|
Th 2/1/07
|
HW due: Read §8-6; write §8-6 #1, 2, 7, 18. Note that #18
is a “thinking problem” that involves no computation. If you disagree with
the question as posed (and I guess I might as well mention that I do), then
feel free to modify the question slightly, or provide a more thoughtful
answer than the canned answer the textbook is obviously seeking.
|
|
|
F 2/2/07
|
No additional HW due. Clean up the existing problems.
If possible, resolve the discrepancy in #18. We achieved an answer of 181.066
by plane slicing but could not match that with cylindrical shells as time ran
out at the end of the period. Please read through the following correction
and be prepared to justify the pieces and parts by Wednesday of next week.
If we let (A, B) be the rightmost intersection point of the two curves, where
points on the left branch of the parabola are of form (x1L, y1),
points on the right branch of the parabola are of form (x1R, y1),
and points on the exponential curve are of form (x2, y2),
then the setup for cylindrical shells should be the following:
∫1B 2prh dy + ∫B5
2prh dy = ∫1B 2p(y + 1)(x2 – x1L) dy + ∫B5 2p(y + 1)(x1R – x1L) dy
= ∫1B 2p(y + 1)[log1.4 y – 2 + Ö(5 – y)] dy + ∫B5 2p(y + 1)2Ö(5 – y) dy
» 75.287 . . . + 105.778 . . . = 181.066
Hooray!
|
|
|
M 2/5/07
|
HW due: Skim §8-7 (reading notes optional this time); write
§8-7 #1-4 all, 21, 22, 24, 27, 31.
Today is a normal class period. Anyone taking a cut or a skip today should
e-mail his HW by no later than noon today. Remember to put a double
underscore at the beginning of your subject line. In your e-mail, you may omit
the graphs, and you may be creative in your typographical approach. For
example, here is how you might write up #5 for e-mail:
5.(a) Shown only on paper version (omitted for e-mail).
(b) L = integral from 1 to 6 of sqrt(1 + (2x-5)^2) dx =
15.8617 . . .
(c) From (1,-1) to (2.5,-3.25) is about 2.7 units by
distance formula (Pythag. Thm.).
From (2.5,-3.25) to
(6,9) is about 12.7 units by distance formula.
Both are
underestimates, using secants (chords). Thus the true answer is somewhat
larger than 2.7 + 12.7
= 15.4, and the answer of 15.862 is reasonable.
|
|
|
T 2/6/07
|
Go to Trapier Theater for the AMC 10/12, held during
A and B period.
|
|
|
W 2/7/07
|
HW due: Read §8-9; clean up your problems from Monday, especially
#27 (which cannot use the book’s
answer unless you provide all of the simplification steps), and write §8-9
#1, 2, 3, 6.
|
|
|
Th 2/8/07
|
HW due
(optional): Read §§9-2 and §9-3. There
is no need for reading notes this time. Per our agreement, you cannot be
faulted if you skip this assignment, because it was not posted by 3:00 p.m.
|
|
|
F 2/9/07
|
HW due: Read §§9-2 and 9-3; write §9-2 #5, 7, 10, 11, §9-3
#1, 10.
|
|
|
M 2/12/07
|
HW due: Skim §§9-8 and 9-9 (reading notes optional this
time); write §9-8 #4, 5, 10, §9-9 #5, 10, 27, 34.
All you really need to know about hyperbolic functions was covered in class
last Friday. All you really need to know about inverse trig and inverse hyperbolic
function antiderivatives can be summarized by the sentence, “Use integration
by parts.”
|
|
|
T 2/13/07
|
HW due: Find the error in the class work for #10 on p. 471
(extra credit opportunity). But first, do the review problems as listed
below.
p. 432 #T3, T5, T6, T7, T10, T11.
p. 444 #25, 32.
pp. 482-483 #30.
|
|
|
W 2/14/07
|
(Updated 6:20 a.m.) No school today. The test
originally scheduled for today will be posted by noon as a take-home test due
on our next class day. If there are widespread power outages, I will
telephone each of you with even-numbered book problems that will serve as
your take-home test. (If there are power outages that are only in isolated
areas, then you will need to contact a classmate to get a copy of the test.)
(Updated 11:56 a.m.) There seem to be no power problems. It is not a bad day
to be stuck at home. Please download your take-home
test and start working. There is no additional work due tomorrow other
than the test.
(Updated 6:54 p.m.) Here are the point values
and estimated timings, in case you were curious. A fast student who has a
good work area, good lighting, and no interruptions should be able to finish
the test in about an hour. Realistically, 2 hours is more likely, since you
will probably need to move around a bit, and you are permitted to check
answers (numeric answers only) with
classmates. But, looking on the bright side for a moment, 2 hours is only 35
minutes longer than you would normally spend on class time plus homework, and
I know for a fact that some of you sometimes spend longer than 2 hours on
homework alone.
Please read the following.
Whatever you do, don’t drive anywhere! It would be a terrible tragedy if you
were injured or worse on a day when school was closed for your safety.
I am happy to announce that the algebra bug has been found. Can my eyes
really be better than 12 pairs of talented student eyes? No, I think I just
got lucky.
FTC Solution to §9-8 #10:
By cylindrical shells, V = ∫01
2prh dr = 2p ∫01 x tan–1 x dx.
By letting u = tan–1 x, dv
= x dx, integration by parts yields
2p(x2/2 · tan–1 x – 0.5 ∫ x2/(1
+ x2) dx) for suitable limits of
integration. However, as we saw, division allows us to write x2/(1 + x2) as 1 – 1/(1 + x2), which has
antiderivative x – tan–1
x + C.
To summarize, V = 2p((x2/2
· tan–1 x) |01
– 0.5 ∫01 x2/(1
+ x2) dx) = (px2 tan–1
x – p(x – tan–1
x))|01
= p(12) tan–1 1 – p(1 – tan–1 1) – (0 – p(0 – 0)) = p2/4 – p(1 – p/4) = p2/2 – p » 1.793 as required.
|
|
|
Th 2/15/07
|
Take-home test due at start of day: Chapter 8,
plus §§9-2, 9-3, 9-8, and 9-9. Point values and estimated timings are also
available for download.
Note: Class was cancelled today
because of the 9:00 a.m. weather-related start time.
|
|
|
F 2/16/07
|
No school.
|
|
|
M 2/19/07
|
No school.
|
|
|
T 2/20/07
|
HW due: Read the paragraphs below, plus §§9-4 and 9-5; write
§9-4 #1 (follow instructions, but then check answer using formula at top of
p. 449), §9-5 #1-29 odd, and read #35, 36.
Note: Do not actually do #35 and
#36, but please read them to verify that they are somewhat comparable to #1
from your take-home test. If you start to
work these problems, you will notice that the limits for #35 are easier than
in the take-home problem, but the rest of the problem is similar and requires
the green box on p. 452 (which is why that hint was furnished on your
take-home test). As for #36, this problem is easier computationally than the
take-home problem, but the fact that you do not know what you are shooting
for increases the difficulty somewhat. Perhaps I should have given you #35 and
#36 instead of the limaçon problem. One concern I had regarding #36 is that
some people would look up the answer on the Web, but I could have neutralized
the advantage by providing a link to the answer or simply giving you the
answer. However, if the answer is provided, #36 is too easy for take-home
purposes. As an in-class test question, though, #36 is fine as written.
Regarding the take-home test, I received many comments from students,
parents, and my department chairman. Only a small number of these comments
were positive in nature. After the grades are computed (target: end of next
week), we should probably discuss some way in which I can attempt to make
amends, recognizing that no perfect adjustment is possible.
One thing you could do to help me would be to prepare, to the best of your
recollection, a breakdown of the amount of time you spent on each subproblem.
What I suspect may have occurred is that people earned 80% of the points in
the first few minutes and then spent a long period of time (the record was
said to be over 11 hours) tweaking and striving for those last few points.
While our educational system trains you in this strategy, and while there is
nothing wrong with it in principle, the reality is that the time you spend in
one subject takes time away from other subjects. In the work world, there is
seldom time to perform every task with 100% accuracy, and you have to become
comfortable with accepting a lower standard of achievement in the interest of
balance. Remember, we are not perfectionists. (Exceptions include anyone
planning to go into air traffic control, minesweeping, or neurosurgery as a
career. We need and want perfectionism there.)
As for §9-4, we will spend only a small amount of time on reduction formulas.
The basic technique is what we already discussed, namely that of performing
integration by parts in order to create an equation in which the desired
answer, I, shows up on both sides
of the equation so that you can solve for I.
In §9-5, there is nothing really new or earth-shattering except for the green
box on p. 452. You will want to memorize this box and bookmark the page. If
you do not wish to do all of the assigned problems at one sitting, please
break up the assignment and do a little at a time. You need to build proficiency
with the trigonometric functions and identities.
Working Ahead (optional): Since
there is a 4-day weekend, you may wish to work ahead a bit. We are skipping
§9-6 this year, and we have already done §9-8 and §9-9.
|
|
|
W 2/21/07
|
HW due: Patch up yesterday’s problems; read the partial
fractions tutorial from the University of California at Davis; write out
the answers to the first several problems on that Web page (detailed
solutions are provided to help you learn).
Double Quiz (10 pts. each) at
start of class will be on solids of revolution. The difficulty level will be
much easier than the take-home test, in other words comparable to yesterday’s
in-class practice. Time limit will be 5 minutes (total) for setups only, or
10 minutes (total) if number crunching is required.
|
|
|
Th 2/22/07
|
HW due: Read §9-7; write §9-7 #1-14 all (or as many as you
can stand), 20, 23ac, 24. Do not omit 20, 23, or 24.
|
|
|
F 2/23/07
|
HW due: Read §9-10; rewrite §9-7 #20, 24; write §9-10 #1-22
all (or at least as many as you can stand), 24. Do not skip #24, which is one
of the most amazing theoretical calculus problems ever. Problem #24 is not
exactly a real-world application, but you must admit, it makes an interesting
paradox. A finite volume of paint, if forced to seep across an
infinitesimally thick boundary so as to coat the bucket’s surface from the
inside, cannot do the job—an infinite amount of paint is needed, because the
surface area is infinite!
|
|
|
M 2/26/07
|
HW due: Read §9-11 (comprehensive summary of derivatives and
antiderivatives); write §9-11 #1-100 all. To avoid busywork, you may
sometimes write the name of the technique instead of solving the problem,
provided you are confident that you could
solve the problem. Be sure to spot-check answers so that you are not deluding
yourself, however. For problems such as #19, simply write “trig sub.,” since
we did not do §9-6 this year, and move on to the next problem.
|
|
|
T 2/27/07
|
HW due: Chapter test on pp. 501-502, omitting T11a. Please
also solve the following two problems.
1. For an ellipse having semiaxes of length c and d, compute (a)
the circumference (setup only) and (b) the area (setup and computation).
2. Compute the volume of an ellipsoid (wlog) having semiaxes of length a, b,
and c. An ellipsoid is a solid all
of whose cross sections are ellipses, and an ellipsoid centered at (0, 0, 0)
has general equation 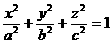 . .
Hints for #1: For part (a), only
the setup is expected. Actually computing the integral wlog is far beyond the
scope of our course. For part (b), it is helpful to know (for example, see
formula #29 on p. 629 of the IntroCal textbook) that
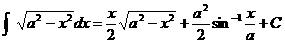 . .
Since this formula requires trig substitution to derive, you may take it as a
given.
Hints for #2: If you cannot solve
#1(b), you should still be able to solve #2. Of course, you will need to look
up the answer to (b) in order to proceed, but since you have a book with an
index (not to mention the Internet), I will expect you to do #2 even if you
failed at #1(b).
|
|
|
W 2/28/07
|
HW due: Read §§10-2 and 10-3. (These will not be on
tomorrow’s test.) Continue working review problems, including the ellipse and
ellipsoid problems posed yesterday.
|
|