|
M 1/1/07
|
New Year’s Day (no school).
|
|
|
T 1/2/07
|
Cathedral funeral for former President Gerald R.
Ford (no school).
|
|
|
W 1/3/07
|
HW due
(strongly suggested): Review for
your midterm exam. After you have spent several hours reviewing, preferably
spread over a period of several days, please attempt this sample midterm exam. We will
spend some time in class discussing some of the answers.
Warning: Every year there are some
students who think they can take a shortcut by skipping the review and
immediately taking the practice midterm exam. This is not a good idea, because
the practice exam is not comprehensive. (Think about it. There is no way to
cram a comprehensive exam into an hour and a half or two hours. We have
covered a huge amount of material since September.) Therefore, if you take
the practice exam and then go back to “plug the gaps,” so to speak, you will
not have made a comprehensive review of the material that is fair game for
the real exam. Plus, since you would have already taken the practice exam,
you would no longer have a valid way to gauge how well prepared you are.
The bottom line is this: Study first, and then take the practice midterm exam
as a way of testing yourself.
|
|
|
Th 1/4/07
|
HW due: Consider the non-separable diffeq. dy/dx
= 7x + 2y with Blount’s initial condition (–2, –3).
(a) Sketch a slope field on the lattice [–4, 4] ´ [–4, 4].
(b) Estimate y when x = –2.45. Show your work. If
possible, do part (b) twice, using a different step size the second time.
(c) Sketch the particular solution as a smooth curve overlaid on your slope
field.
(d) On a fresh grid, sketch the following three particular solutions:
(i) Solution passing through initial condition (–1, 1.7).
(ii) Solution passing through initial condition (–1, 1.8).
(iii) Solution passing through initial condition (–1, 1.9).
In class: Midterm exam review.
|
|
|
F 1/5/07
|
HW due: Track down Blount (or me) and obtain a copy of the
BIGSLOPE program, which plots slope fields and Euler’s method solution
estimates.
In class: OCQ (Oral Cumulative Quiz).
At the beginning of the period, you will receive several thought-provoking
questions. You may discuss the questions or make notes among yourselves, even
including sharing intelligence from previously summoned students. People will
be summoned into the piano room in random order, one by one, and asked a
randomly chosen question from the sheet. Follow-up questions are possible.
Some students will be summoned more than once, either as a result of random
selection or as a way to have a second shot at earning an A.
Ground rules: There will be one
student “on deck” outside the piano room while each student is being quizzed.
All other students must remain in Room 202 with the door closed.
Assembly period: During the first
15 minutes of the assembly period, we will meet in Room R to continue the OCQ
if necessary. Each student will also be required to ask me one substantive
question during that time. (Do not ask about the time, date, location or
format of the midterm exam. The time, date, and location are published, and
the format will be similar to that of the sample exam provided, except that
there will be some multiple-choice questions as well.)
Sample questions: Here are two
sample questions. The difficulty level of the OCQ will be at or slightly
below the level of these questions.
1. Let f, g, h be differentiable
functions of t such that the first
derivatives at all values of t, as
well as the value of the ordered triple (f
(0), g(0), h(0)), are completely known. Explain how to find the ordered
triple (f (2.2), g(2.2), h(2.2)). Of what possible real-world usefulness is this?
2. Let f be a Riemann integrable
function that is defined by a formula, although the formula is expensive to
compute. Does it matter whether we use upper or lower Riemann sums to
estimate ∫ab
f (x) dx? In what sense is
this an ill-posed question?
Questions for clarification:
Sometimes you can reveal a lot about what you know by the types of questions
you ask for clarification. Here are some things you might ask about #1 above.
“What do you mean by ‘first derivatives at all values of t’?” This is a weak question, since the first derivative has been
previously defined as the limit of a difference quotient, and the phrase “at
all values of t” is a standard way
of expressing the domain of these derivative functions. It sounds as if the
student is stalling for time.
“What do you mean by ‘real-world’?” This is a fair question, but by now the
student should know that most real-world applications of the calculus involve
physics, engineering, meteorology, chemistry, biochemistry, or sports.
“What do you mean by ‘completely known’?” This is a better question, since
the phrase is somewhat ambiguous. However, the student is only revealing his
confusion, not suggesting a way of resolving the confusion.
“By ‘completely known,’ do you mean defined by a table of values, defined by
a set of formulae, or something else—an accurate graph, perhaps?” This
student has clearly thought about the question and what will be needed to
solve it. He also knows about the rule of GNAV and might be able to give a
good answer to question #1 as soon as the teacher clears up the ambiguity.
|
|
|
F 1/5/07
|
During
lunch, during E period, or after school (approx. 3:00 p.m.): Optional second try for Blount, Michael, Lenny,
Kevin.
|
|
|
W 1/10/07
|
Midterm
Exam, Steuart 102, 8–10 a.m.
Because nobody contacted me before the deadline on Wednesday, Jan. 3, there
will not be an alternate time for the exam. If you have a conflict, you will have
to negotiate something with your other teacher.
Note: Part of the exam will be
taken directly from the OCQ. Typos in the
instructions, question #1, and question #3 have been corrected. A complete solution key is also available now.
|
|
|
M 1/15/07
|
No school (holiday for Dr. Martin Luther King, Jr.).
|
|
|
T 1/16/07
|
No school (faculty professional day).
|
|
|
W 1/17/07
|
HW due: Show all work as you complete the following two
problems. Answers that are not supported by work will not be accepted. You
may compare answers with friends, but your work must be your own.
|
|
|
|
1. 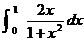 equals equals
|
|
|
|
(A) 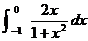
(B) 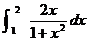
(C) 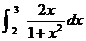
|
(D) 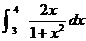
(E) 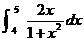
|
|
|
|
2. Compute 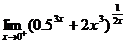 . Please note, the expression . Please note, the expression 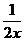 is an exponent,
not a factor. is an exponent,
not a factor.
|
|
|
|
(A) ½
(B) 1
(C) 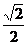
|
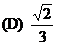
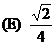
|
|
|
Th 1/18/07
|
HW due: §7-5 #8, p. 342 #R4, R5, R6.
|
|
|
F 1/19/07
|
HW due: Read §8-2; write §8-2 #2-28 even. Also revisit #8b
from yesterday’s set.
|
|
|
M 1/22/07
|
No additional HW due. Please use the weekend to
patch up the gaps in your previously assigned HW.
|
|
|
T 1/23/07
|
HW due: Read §8-3; write §8-3 #2, 4. These are relatively
straightforward problems, but I want to see how well you write up word
problems. Remember, the goal is communication,
not merely getting the “right answer.”
|
|
|
W 1/24/07
|
HW due
(optional): Rewrite #2 and #4 so
that they use the “Minimize [or maximize] W(x) = _____ s. t. _____” format that we
discussed yesterday while the classroom was in darkness. Then answer one of
the remaining questions in §8-3, since any of them would be a good candidate
for a test problem, plus the following thought problem:
1. What do you think is meant by the term “suboptimization”? Which of the
several optimization procedures we discussed—linear programming, nonlinear
programming, dynamic programming, heuristic programming—is most likely to be
plagued by the problem of suboptimization?
|
|
|
Th 1/25/07
|
HW due: Read §8-4; write §8-4 #10, 13-16 all, and prove
that the area of any triangle is bh/2,
where b = width of base, h = height.
Hints for the last problem: Of course
you can do this using geometry. That is not in question. I want to see if you
can solve this as a parameterized calculus problem instead. Wlog, let the
interval [0, b] on the x-axis be the base, and again wlog,
let (a, h) be the coordinates of the triangle’s third vertex for some
real number a and some positive
real number h. You will need to
make a sketch and satisfy yourself that the situation truly is wlog. Find
equations for the two non-base sides of the triangle. Then rewrite those
equations as equations in which x
is expressed as a function of y.
Let us call x1 the
function for the left side of the triangle (i.e., the side that passes
through the origin), and let x2
be the function for the right side of the triangle (i.e., the side that
passes through the point (b, 0)).
It is important to note that you must express both x1 and x2
as functions of y.
Having done all the steps above, you may write the area of the triangle as ∫0h (x2 – x1)
dy. I have done the entire problem
for you except for about 3 lines of algebra.
Challenge problem (optional):
Prove that the area under a parabolic arch is 2bh/3, where b = width
of base, h = height to vertex. Note
how similar this is to the previous problem.
|
|
|
F 1/26/07
|
HW due: Read §8-5; write yesterday’s challenge problem as a
required problem, plus §8-5 #1, 2. For both #1 and #2, you will be
integrating pr2 with
respect to y, where the radius must
be given as a function of y.
Challenge problem (optional):
Prove the formula from geometry class for the volume of a general right
circular cone with radius r and
height h. In other words, repeat
#2a wlog.
|
|
|
M 1/29/07
|
HW due: Write §8-5 #20, 26; p. 428 #R2d (without
calculator!), R3b, R4ab.
|
|
|
T 1/30/07
|
Quest (70 pts.)
on §§8-1 through 8-5. To help you
as you study, the solution to #26 from yesterday’s HW is provided below.
26. Let y = height of isosceles
trapezoid shown, and let 50 + 2z =
distance across top of isosceles trapezoid shown, where z = y tan 38° by basic
trigonometry. Then area of trapezoid = ½(b1
+ b2)h = ½(50 + 50 + 2z)y = (50 + z)y
= 50y + y2 tan 38°. Thus a thin cross section of thickness dx has volume
dV = (50y + y2 tan
38°) dx
from which we get V = ∫0600
(50y + y2 tan 38°) dx,
which can be approximated by the trapezoid rule. Letting the integrand be A(x),
we have
V » ½ Dx (A(0) + 2A(30) + 2A(60) + 2A(90) + . . .
+ 2A(570) + A(600))
» ½(30) ( (50(0) + 02 tan 38°) + 2(50(5) + 52
tan 38°) + . . . + (50(0) + 02 tan 38°) )
» 15(0 + 2(269.532) + 2(513.284) + 2(925.789) + . . . + 2(853.132) +
0)
» 1,649,443.654 yd3
At $12.00 per cubic yard, this comes out to be about $19.793 million.
|
|
|
W 1/31/07
|
HW due: Re-do yesterday’s quest completely, even the parts
that you think you did correctly. (This was a book test, which means I can’t
post it on the Web. If you have lost your copy, please get one from a
classmate.) Show all work neatly.
My intention is that this HW assignment will count more than the quest
itself. You may compare answers and discuss solution techniques with friends,
but no copying is permitted. Your writeup must be your own.
Sloppy or disorganized submissions, or submissions that do not adhere to the
standard HW format, will not be graded. Please have your papers ready to hand
in when class begins.
|
|