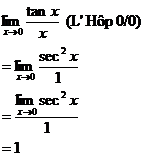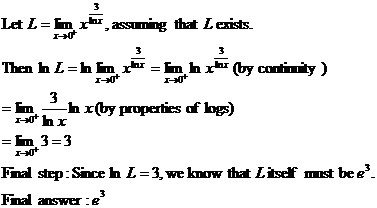Monthly Schedule

(Honors AP Calculus BC, Period A)

F 12/1/06

HW due: Write §6-9 #1-30 all.

 

M 12/4/06

HW due: Write §6-8 #3-27 mo3, 31; §6-9 #31-60 all. Please follow the examples below when writing up your L’Hôpital’s Rule problems. There are several points to keep in mind if you wish to earn full credit on quizzes and tests:

1. Indicate the place(s) at which you “hop” to the next step by means of an application of L’Hôpital’s Rule. Otherwise, the reader may lose the thread of your derivation, since L’Hôpital’s Rule is not a run-of-the-mill algebraic transformation.

2. Indicate the indeterminate form (0/0 or ¥/¥) that justifies the application, since as you know, L’Hôpital’s Rule can be applied only if you have one of those two basic forms.

3. Remember to repeat the word “lim” (written in cursive) throughout the derivation. It is not correct, for example, to say in problem #3 that (tan x)/x = (sec2 x)/1 = 1.

4. Technically, the chain of equal signs ( = ) in a L’Hôpital’s Rule derivation should be “question mark equal signs,” since we do not know until we reach a finite limit at the end that the initial limit actually exists. If the final answer in the chain is DNE, then L’Hôpital’s Rule gives no information, and we must use another method of analysis to determine the limit. However, I will allow you to use equal signs.

Worked examples:

3.












27.










Note that we never needed L’Hôpital’s Rule in #27. However, for most of these problems, you will need to use L’Hôpital’s Rule one or more times.

 

T 12/5/06

HW due: Finish loose ends (if any) from yesterday’s assignment; then write §6-8 #30, 32; §6-9 #61-90 all.

 

W 12/6/06

HW due: Review problems on p. 302 #T7-T18 all.

In class: Review.

 

Th 12/7/06

HW due: General binder check.

Test on Chapter 6. This test will not be averaged, since your previous quiz has not yet been graded following the funeral. However, I will evaluate the scores to see how you are doing. Problems will be comparable to the review problems on pp. 297-299, plus you are responsible for statements and proofs of the change-of-base formula and the chain rule for integrals.

 

F 12/8/06

HW due: Read green box on p. 309 and all of §7-2; write §7-2 #Q1-Q10 all, and make up a grading key (with partial credit rubric) for yesterday’s test. Each problem is worth 10 points. For example, for #4 you could write something like this:

#4. Correct answer: (ln |sec x3 + tan x3|)/3 + C. Deduct 2 pts. if student forgot the “+ C” / 4 pts. if student forgot to divide by 3 / 2 pts. per other small error. No credit if answer is wrong and shows no work indicating knowledge of u substitution.

 

M 12/11/06

HW due: §7-2 #1, 2.

 

T 12/12/06

HW due: Read §7-3 (notice how the examples demonstrate the “plugging in” procedure we discussed yesterday in class—reading notes are optional this time); write §7-3 #3, 4.

 

W 12/13/06

Test on Chapter 6. This will be similar to last Thursday’s test and will be counted.

 

Th 12/14/06

No additional HW due. However, since we resolved the algebra tangles in §7-3, you are expected to have complete (and essentially correct) responses to the §7-3 problems. They may be spot-checked.

 

F 12/15/06

HW due: Attend the Service of Lessons and Carols on Thursday night (expected of everyone).

 

 

Return to the HappyCal Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 04 Jan 2007