|
W 11/1/06
|
HW due: Read §5-4 (optional); write §5-3 #8-38 even (as
announced in class).
|
|
|
Th 11/2/06
|
HW due: Read §5-4; write §5-4 #3-42 mo3, 43, 44, 46.
After HW check: “Fun Friday on Thursday.”
|
|
|
F 11/3/06
|
No
school.
|
|
|
M 11/6/06
|
HW due: Read §§5-5 and 5-6. Celebrate the long weekend with
no written work (except for your reading notes, of course). There may be a
short open-note quiz today.
In class: Work period necessitated by underengineering of Mr. Hansen’s tire
iron and car jack.
|
|
|
T 11/7/06
|
HW due: §5-5 #11, §5-6 #3-6 all, 12, plus the following
four supplementary questions.
The hypotheses of MVT are often stated correctly in the following way: Let
function f be continuous on [a, b]
and differentiable on (a, b). Show, by means of a sketch in each
case, that the MVT conclusion need not be true if the hypotheses are altered
as follows:
S1. Let function f be continuous on
[a, b].
S2. Let function f be continuous on
(a, b) and differentiable on (a,
b).
S3. Let function f be integrable on
[a, b] and differentiable on (a,
b).
S4. Let function f be
differentiable on (a, b).
|
|
|
W 11/8/06
|
HW due (optional): p. 166 #9; p. 172 #28ab; pp. 217-218 #1, 3, 4; p.
241 #R2, R3, R4, R5ab.
In class: Review.
|
|
|
Th 11/9/06
|
Test
(cumulative through §5-8). The emphasis
will be on §§4-7 through 5-8, but you cannot forget important earlier
material, e.g., the green boxes on pp. 142, 148, and 150. HappyCal is a
cumulative class, and it would be a mistake to think that you could prepare
yourself well for a test on §§4-7 through 5-8 by “cramming” the contents of
those sections.
|
|
|
F 11/10/06
|
HW due: Redo the entire test
from yesterday.
Guest speaker (F period): If you are interested in nanotechnology and are
free during F period, come to Steuart 202 at 12:45 to hear Dr. David Nagel, a
nanotechnology researcher from George Washington University. Invite your
friends!
|
|
|
M 11/13/06
|
HW due: Read §5-9; write §5-9 #3-21 mo3, 23-27 all, 31-36
all.
|
|
|
T 11/14/06
|
HW due: Read §5-10; write §5-10 #3, 4, 5, 7.
|
|
|
W 11/15/06
|
HW due: Read §6-3; write §5-11 #3, §6-1 #1-3 all, §6-2 #1-5
all, §6-3 #3-45 mo3, 47, 48. If time is short, you may omit a few of the §6-3
problems without penalty, but please try to do them all as a way of building
endurance and proficiency.
Challenge Problem: Unscramble
SDBIRAE to find a word that means “secondary discussion.”
|
|
|
Th 11/16/06
|
Quest on Chapter 5 (50 pts.). Material will be similar to that seen last week, except
with more problems on definite integral computation, variable-factor
products, and Simpson’s Rule.
Since we have not discussed Simpson’s Rule much, here is a completely worked
example problem (#3 from §5-11):
(a) Scatterplot:
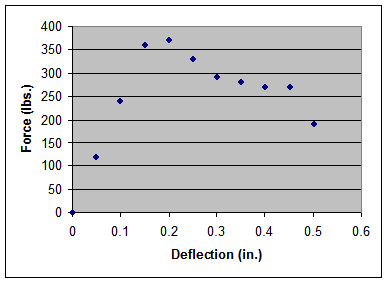
(b) dW = F dx where force (F) is
a variable factor and dx denotes an
infinitesimal bit of displacement (i.e., deflection of the bar)
Therefore, W = ∫00.5 F dx, but since we have no formula for the force function F, we must use a quadrature method to
estimate the definite integral. For fun, let us compare the results of the
Trapezoid Rule with Simpson’s Rule.
W » ATrap.
Rule = Dx/2 (F(0) + 2F(0.05) + 2F(0.10) + . . . + 2F(0.45)
+ F(0.5))
= Dx/2 (0 + 2(120) + 2(240) + 2(360) + . . . + 2(270) +
190)
= 0.05/2 (0 + 240 + 480 + 720 + . .
. + 540 + 190)
= 0.025 (5250) = 131.25
inch-lbs.
W » ASimp.
Rule = Dx/3 (F(0) + 4F(0.05) + 2F(0.10) + 4F(0.15) + .
. . + 4F(0.45) + F(0.5))
= Dx/3 (0 + 4(120) + 2(240) + 4(360) + . . . + 4(270) +
190)
= 0.05/3 (7970) » 132.833 inch-lbs.
Which result is more accurate? There is no way to know for sure. However,
since the force is probably nonlinear over most of its domain, it is likely
that the Simpson’s Rule approximation is better. The Trapezoid Rule, after
all, assumes that the force function is linear between mesh points.
One criticism of Simpson’s Rule is that it permits nondifferentiability at
the mesh points, even though most real-world functions would be
differentiable throughout much of their domain. (In the present problem, for
example, differentiability would be violated at places where a sudden
splintering or giving way occurred, but elsewhere differentiability would
probably be maintained.) If this objection must be overcome, there are other
types of functions you could study, called splines, that not only pass through the known data points but
preserve differentiability as well. Splines are not as easy to integrate as
the parabolas used in Simpson’s Rule, but they are not particularly hard,
either. For example, a program to integrate cubic splines using FTC1 would be
fairly easy to write. Antiderivatives of cubic splines are simply quartic
polynomials, which are easy for a computer program to evaluate.
One thing we can say is that for functions that are specified by a formula,
Simpson’s Rule converges to the true definite integral value much faster than
any of the “plain” Riemann sums do (left endpoint method, right endpoint
method, midpoint method, upper sum, lower sum, etc.). Since the Trapezoid
Rule is the mean of the left endpoint and right endpoint methods, Simpson’s
Rule also beats the Trapezoid Rule in terms of accuracy for a given mesh
size.
Interesting Side Note: Simpson’s
Rule can be shown to be equivalent to the weighted average (2M + T)/3, where M denotes
the result of a midpoint method and T
denotes the result of the Trapezoid Rule. We should do this someday in class.
|
|
|
F 11/17/06
|
HW due:
1. Prove the “interesting side note” from yesterday’s calendar entry. This is
an algebra exercise that involves practice with the notation. Because it
reinforces the meanings of the midpoint and Simpson approximations, it is
educationally worthwhile. Hint:
Start with an even number of points, numbered 0, 1, 2, 3, 4, . . . , 2n. Use the even-numbered points as
mesh points for Simpson’s Rule, and use the odd-numbered points as the
midpoints of the intervals. (There are n
intervals in all.) What additional condition must you impose on n so that Simpson’s Rule will work out
correctly?
2. Do problem 2abc from yesterday’s quest (reproduced below).
|
|
|
|
The
weight of a bucket is an approximately quadratic function of its height h above ground. (See table at right.) Estimate
the work performed in lifting the bucket to a height of 3 feet. Use (a) the
Trapezoid Rule with 4 intervals (i.e., 5 mesh points), (b) Simpson’s Rule
with 4 intervals (i.e., 5 mesh points), and (c) Simpson’s Rule with 2
intervals (i.e., 3 mesh points).
|
Height
(ft.)
0.0
0.375
0.75
1.125
1.5
1.875
2.25
2.625
3.0
|
Weight
(lbs.)
9.0
8.8969
8.7375
8.5219
8.25
7.9219
7.5375
7.0969
6.6
|
|
|
|
3.
(Extra credit.) One of the problems on yesterday’s quest was to compute 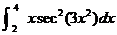 . .
What happens when you compute this using your calculator? Explain why FTC1
does not apply here. (This was a mistake on my part.) What is the correct
answer to the problem?
|
|
|
M 11/20/06
|
HW due: Read §6-4; write §6-3 #49-54 all, 58.
|
|
|
T 11/21/06
|
HW due: Read §6-5; write §6-5 #1-18 all, 20-32 even.
|
|
|
Break
|
Happy Thanksgiving. If you have a chance, please say
a prayer for my mother-in-law, Judith Mosier, who suffered a severe stroke
Nov. 19. Emergency surgery on Nov. 20 saved her life, but we do not yet know
if she is going to recover.
|
|
|
M 11/27/06
|
No additional written HW due. Please enjoy your
Thanksgiving break, and if you have any spare time, please use it to finish up
any previously assigned problems that you could not finish on the first try.
|
|
|
T 11/28/06
|
HW due: Read §6-6; write §6-6 #17, 18.
|
|
|
W 11/29/06
|
HW due: Read §6-7; write §6-6 #5-16 all, 19.
|
|
|
Th 11/30/06
|
HW due: Read §6-8; write §6-7 #3-54 mo3.
|
|
|
|
|
|
|
