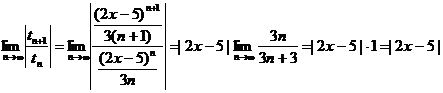|
T1.
|
Sketch the function 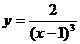 , and sketch rectangles underneath the curve in such , and sketch rectangles underneath the curve in such
a way that the first rectangle (from x
= 1 to x = 2) has height 2, the
second rectangle (from x = 2 to x = 3) has height 2/8, and so on. The
1000th rectangle, from x = 1000 to x = 1001, therefore has height 2/10003.
You should write a line of explanation stating that the function is an upper
bound for the height of each rectangle, and therefore 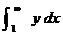
is an upper bound for the series. The series equals the sum of rectangular
areas, namely 2 + 2/8 + 2/27 + 2/64 + . . .
Thus 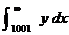 is an upper bound
for the tail of the series after 1000 terms. By is an upper bound
for the tail of the series after 1000 terms. By
techniques of improper integrals that we learned earlier in the course
[omitted here since you are supposed to be able to do this by now], the upper
bound is 10–6.
|
|
|
|
|
T4.
|
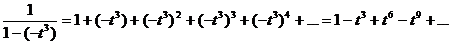
Integrate term by term to get the answer: 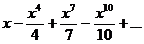
Do you see why the constant term in this series must be 0?
|
|
|
|
|
T5.
|
Because this is a geometric
series with common ratio r = –t3, we have convergence iff
|r| = |–t3| < 1, which means –1 < x < 1.
|
|
|
|
|
T11.
|
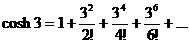
The nth term (where n = 0, 1, 2, ...)
is of form 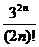 , ,
which is a simplification of the Taylor term 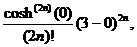
since all of the even-numbered derivatives of the cosh
function are cosh functions, and cosh 0 = 1. However, since half the terms are missing
because they are 0, and since we started at 0, the number of terms is not n but rather n + 1. The remainder term after n + 1 terms is therefore
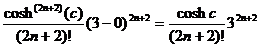 , where c is some
number between 0 and 3. , where c is some
number between 0 and 3.
This expression, which is positive, is by definition 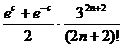 . .
Since ec
is maximized when c = 3, and since e–c is maximized when c = 0, and since e < 3, we can obtain a “non-cheating” bound:
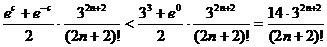 . .
That last expression first falls below .5 · 10–10 (half the place
value of the 10th decimal place) when n
= 11. Since we saw above that the number of terms is n + 1, our final answer is 12.
|
|
|
|
|
T14.
|
Use the Ratio Test:
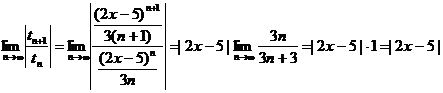
This final expression, |2x – 5|, is
what we want to be < 1. Solving the inequality [boring algebra
omitted] leads to 2 < x < 3.
The radius of convergence is 1/2 by inspection. As for the issue of
convergence at the endpoints of the interval, that is addressed in the next
problem.
|
|
|
|
|
T15.
|
For x = 2, the series becomes 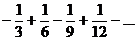 , which converges by AST. , which converges by AST.
[You should practice checking the 3 conditions and documenting in writing that all 3 are satisfied:
strictly alternating signs, absolute value strictly decreasing, limit of
absolute values equaling 0.]
For x = 3, the series is 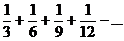 , which is a systematic proper subset , which is a systematic proper subset
(every third term) of the harmonic series, hence divergent. If you do not
like that explanation, note that you can factor out 1/3 to get
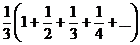 , where the second , where the second
factor diverges since it is precisely the harmonic series.
Final conclusion: Interval of convergence is [2, 3).
|