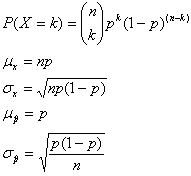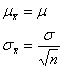Test #6, 2/23/2006

STAtistics / Mr. Hansen
2/23/2006

Name: _________________________

Test #6

Sampling distributions, t procedures, confidence intervals, etc.

Time limit: 34 minutes (51 for extended time).

Useful Formulae:

	P(A È B) = P(A) + P(B) – P(A Ç B)

	E(X) = m_X = S x_ip_i


	If X has a binomial distribution with parameters n and p, then:

	If X has a normal distribution with mean m and standard deviation s, then:




	(See additional formulae and tables on sheets provided at end of textbook.)

1.	How are the sampling distribution of (single sample) and the sampling distribution of (single sample) most accurately described?
	(A) t and normal, respectively (B) t and t, respectively (C) t and binomial, respectively	(D) binomial and t, respectively (E) binomial and normal, respectively

2.	We poll an SRS of 500 voters in a large city and discover that 322 of them think that Candidate Jones is supercilious. A writer for the city newspaper estimates that the true proportion of voters in the city who think Candidate Jones is supercilious is between 63.4% and 65.4%. With what confidence can she make this statement?
	(A) 36% (B) 42% (C) 48%	(D) 95% (E) 98%

3.	In #2, the m.o.e. stated by the writer is
	(A) 1% (B) 2% (C) 4%	(D) 64.4% (E) 65.4%

4.	By default (i.e., unless otherwise stated), political polls in The Washington Post that are reported with a margin of error have a confidence level of . . .
	(A) 90% (B) 95% (C) 99%	(D) 99.9% (E) 100%

5.	I hope that my true mean diastolic blood pressure is no more than 80 mm Hg. Over a period of time, I take 5 measurements at random intervals and find a mean of 78 mm Hg with a standard deviation of 6 mm Hg. Assuming that my blood pressure has a normal distribution, compute a 90% confidence interval for the true mean.
	(A) 72 to 84 (B) 72.28 to 83.72 (C) 72.52 to 83.48	(D) 72.61 to 83.39 (E) 73 to 83

6.	In #5, what is the standard error?
	(A) 2.015 (B) 2.132 (C) 2.683	(D) 2.748 (E) 5.721

7.	In #5, with what confidence can I say that my true mean blood pressure reading is below 80?
	(A) 60% (B) 65% (C) 70%	(D) 75% (E) 80%

8.	Confidence interval statements are always predictions concerning
	(A) statistics (B) parameters (C) raw data	(D) text fields (E) probabilities

9.	Give the approved wording for any problem involving a confidence interval, where the confidence level is 85%.
	(A) “There is an 85% probability that . . .” (B) “The odds are .85 that . . .” (C) “The odds are 85 to 15 that . . .” (D) “We are 85% confident that . . .” (E) “There is at most a .85 probability that . . .”

10.	What is a sampling distribution?
	(A) the distribution of values in a sample (B) the distribution of data in a population (C) the distribution of all possible values for a statistic, when the sample size is variable (D) the distribution of all possible values for a statistic, when the sample size is fixed (E) the distribution of values that a statistic attains under 100 repeated trials

11.	Why is it of crucial importance to study and understand sampling distributions?
	(A) It is not of crucial importance. (B) Sampling distributions are the key to inferential statistics. (C) Sampling distributions allow us to estimate statistics accurately. (D) Sampling distributions allow us to make probability statements regarding parameters. (E) Sampling distributions allow us to determine the size of a sample.

12.	An Independent poll of the Upper School (N = 308) finds that 40% of the 30 students polled (drawn primarily from the senior class) favor a reinstatement of the sock rule. Compute a 95% confidence interval for the true proportion of Upper School students who feel this way.
	(A) 20% to 60% (B) 22.5% to 57.5% (C) 25% to 55%	(D) 27.5% to 52.5% (E) none of these

13.	An Independent poll of the Upper School (N = 308) finds that 40% of the 30 students polled in an SRS favor a reinstatement of the sock rule. Compute a 95% confidence interval for the true proportion of Upper School students who feel this way.
	(A) 20% to 60% (B) 22.5% to 57.5% (C) 25% to 55%	(D) 27.5% to 52.5% (E) none of these

14.	A poll is supposed to estimate the proportion of voters who are in favor of a controversial measure that has divided the electorate approximately into two equal factions. How large an SRS is needed to keep the m.o.e. at or below 2.5%? (Assume a 90% confidence level.)
	(A) 1008 (B) 1083 (C) 1146	(D) 1288 (E) 1301

15.	In #14, how much larger must the sample be if all conditions of the problem remain as stated, except that the m.o.e. is reduced to 0.5%?
	(A) twice as large (B) 5 times as large (C) 15 times as large	(D) 25 times as large (E) 200 times as large