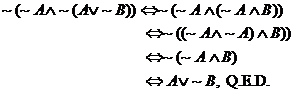STAtistics / Mr. Hansen
12/12/2005

Name: _________________________

Key to Test #3

Probability, symbolic logic, random variables, LOLN, Type I/Type II error, PPV, and simulations
Note: Simulations were on the list of topics, but most of you noticed that there was no room to squeeze a simulation question onto this test. (However, a few of the make-up tests had a simulation question.) The topic of simulations is fair game for the Jan. 5 test as well as for the midterm exam.

Part I: Translations into English.

 

 

 

 

1.

The expected value of a sample mean equals the population mean.

2.

The expected value of random variable X, also called the mean of X, equals the probability-weighted sum of numeric outcomes. Also acceptable: the sum of products formed by multiplying each numeric outcome by its probability of occurring.

3.

The variance of r.v. X equals the probability-weighted sum of squared deviations from the mean of X.

4.

The conditional probability of event A, given that event B is true, equals the probability that A and B both occur divided by the probability of B.

 

 

Part II: Symbolic Logic.

 

 

5.

 

 

 

 

 

6.

A

B

~A

~B

A  ~B

~(A~B)

~A ~(A~B)

~(prev. col.)

 

1

1

0

0

1

0

0

1

 

1

0

0

1

1

0

0

1

 

0

1

1

0

0

1

1

0

 

0

0

1

1

1

0

0

1

 

 

 

Since the last col. is equivalent to the fifth col. for all possible values of A and B, the proof is complete. (Q.E.D.)

 

Part III: Short Answer.

 

 

7.

B(12, 0.85); i.e., binomial with n = 12, p = 0.85

8.

geometric, n = undefined or DNE, p = 0.85

9.

P(X < 9) = 0.092 = the probability that Carl sinks fewer than 9 free throws in 12 tries

10.

 1.176

 

 [this is a formula you are not responsible for knowing]

11.

 = 10.2 [by the formula np, which you were not required to show]

12.

 = 1.237 [by the formula , which you were not required to show]

13.

P(Y > 2) = 0.0225 = the probability that Carl’s first success occurs on or after the third shot

14.

P(63 < Z < 68) = 0.673 = the probability that a randomly selected adult Amer. woman is between 63 and 68 inches tall

15.

No, Z is a normally distributed r.v.

16.

P(at least one crash) = 1 – P(no crashes) = 1 – (0.99999954000)365 = 0.518

17.

H0: subject is not infected

18.

1 – 0.98 = 0.02 = P(Type I error), the probability of a false positive

19.

1 – 0.97 = 0.03 = P(Type II error), the probability of a false negative

 

 

Part IV: Free Response.

 

 

20.

PPV = P(infected | positive reading) = P(infected  positive)/P(positive)
         = 0.00776/0.0276 = 0.281

That is the “textbook” solution to the problem, using the conditional probability formula. However, I’ll be honest with you. I have never liked that approach. Students also tend to dislike using the conditional probability formula here, because it involves a couple of probability calculations and a messy division of decimals.

A tree diagram, in my opinion, makes the problem much easier. Start with a large number of hypothetical people (say, 1 million), and remember to make your first split on whether people are truly infected or not.

 

 

 

 

 

 

The diagram shows a total of 27,600 people with positive readings. Of these, only 7760 are true positives; the other 19,840 are false positives. The probability that a person is truly infected, given that he or she has a positive test result, is therefore 7760/27,600 = 0.281.

 

 

BONUS

PPV = positive predictive value