|
W 2/1/06
|
HW due: Read this
article from yesterday’s Post
and take reading notes for a possible short quiz. Also prepare a statement of
a problem that you feel is of interest for an in-class simulation exercise.
(I gave the example of computing the probability that brothers are randomly
seated at the same lunch table. Do not use my example; make up one of your
own.)
|
|
|
Th 2/2/06
|
HW due: Write a first draft of a methodology for a simulation
to address your problem that you came up with in yesterday’s assignment.
There should be multiple steps, written out clearly and legibly, in
sufficient detail so that an AP Statistics student from a different part of
the country could perform your simulation if necessary. In most cases this
will mean at least 6-8 steps and some charts or tables showing how data
should be recorded and tabulated.
|
|
|
F 2/3/06
|
HW due: Write a draft methodology for the simulation
problem involving Jeter’s 0-for-33 slump. If he is a .313 hitter, how often
would we expect to see such a slump occur in a career if the trials are
independent? Record your assumptions and indicate your steps clearly.
Quiz on Excel (basic concepts only).
|
|
|
M 2/6/06
|
HW due (optional for 2 bonus points): Send me an e-mail, timestamped no later than noon
today, in which you describe your reaction to the new attendance policy. In a
nutshell, it is that people with good lunch attendance records who skip lunch
(unexcused or a cut not cleared through Mr. Andreoli) will receive a small
point penalty, and people with poor lunch attendance records who skip lunch
will receive a larger point penalty. I have also stated that I will rescind
the policy if and when your senior class steps up to the plate and manages to
get the skipping problem under control. If you have an alternative plan to
suggest, then please feel free to mention it. My calculus class has already
suggested one alternative plan, and I am curious to know if you have any
suggestions.
|
|
|
T 2/7/06
|
Double HW due: Modify the Jeter1.xls
spreadsheet to answer the following questions:
1. In a career of 6000 at-bats, what is the probability that a .265 hitter
would experience at least one batting slump of length 30?
2. In a career of 6000 at-bats, what is the probability that a .315 hitter
would experience at least one “hot streak” of 10 hits in a row?
For each question, state the
assumptions of your simulation and describe exactly which cell(s) of the
spreadsheet you are modifying, and in what way. Use a handwritten table to
summarize your tallies of trials and successes. Without these features, your
HW assignment will not qualify for credit.
If you would like to work with the Jeter2.xls
spreadsheet, which has 60,000 rows, you may. However, the download time may
be prohibitive unless you have a fast DSL connection. Also, the 6000-row
spreadsheet is probably more useful for answering questions 1 and 2.
The formulas you will find most useful are RAND, IF, COUNTIF, and SUM. You
can select a contiguous group of cells by using CTRL+SHIFT+arrow key. (For
example, CTRL+SHIFT+DOWN ARROW to select from current cell to the last
occupied cell in the current column.)
|
|
|
W 2/8/06
|
HW due: Starting on p. 475, identify 10 multiple-choice
questions that would be suitable for Friday’s test on null and alternative
hypotheses, Type I and Type II error, sampling distributions, and
simulations. Do not include #1 and #4, which we have already discussed. Show
your work as you answer each question.
|
|
|
Th 2/9/06
|
HW due: Visit the RVLS
sampling distribution simulation. Define an ugly-looking underlying data
distribution, and sketch the sampling distributions of at least 3 different
statistics for each of 3 different sample sizes (a total of at least 9
sketches). Write a paragraph to describe your findings.
You are encouraged to explore the rest of the RVLS (Rice Virtual Laboratory
in Statistics), including the glossary and the online text. See link under
“Essential Links” on the STAtistics Zone page.
In class: Review.
|
|
|
F 2/10/06
|
Test. Material covered will include null and alternative
hypotheses, Type I and Type II error, sampling distributions, and
simulations. Probability (e.g., conditional probabilities, poker
probabilities) may also be tested.
|
|
|
M 2/13/06
|
HW due: Read pp. 248-251. (If you are behind on your reading,
use this opportunity to get fully caught up through p. 251.) Also come up
with a completely correct set of answers to Friday’s
test. You may confer with classmates, but if you don’t know why the correct answer is what it is
when I call on you, you will not receive full credit.
As you try to assemble a perfect set of answers, please argue with your
classmates! Arguing is a great way to learn, since your emotions are
involved. (And as you recall, emotion is the key to learning.) There were no
perfect papers, but every question had at least some people who got it right.
|
|
|
T 2/14/06
|
HW due: Since nobody had a completely correct set of
answers yesterday for Friday’s test, we will try
again today.
Quiz today on the most recent Unconventional
Wisdom column (which has now moved to one day per week on page A2).
|
|
|
W 2/15/06
|
HW due: Show work
and answer pp. 252-255 #1-15 all. Do not copy the book’s work unless you
literally cannot figure out how to proceed. Actually write out a solution to
each problem to the best of your ability before peeking at the answers. (Or
guess, and give a coherent reason for your guess.) Each time you make a
mistake, write a sentence labeled “M” (for metaknowledge) in which you
describe what you learned.
|
|
|
Th 2/16/06
|
HW due: This is a two-part assignment and will be scored as
a double homework. Do both parts.
1. Enter numbers in columns C and D of this
spreadsheet. (Simply overtype the entries that are currently there.) If
you have a comment, such as a suggestion for how one of the proposed
statistics could be improved, please enter that in column E. When you have
finished, e-mail a text extract of the spreadsheet to me. DO NOT SEND THE SPREADSHEET FILE
ITSELF. SEND ONLY THE EXTRACT. Instructions for preparing the extract
are given below.
2. On a piece of paper, with no name written at the top, come up with one or
two additional suggestions for statistics that might be worthwhile for the
school to gather. When I check your homework, I will look to see if you did
this, but then I will immediately place your paper in a big pile and shuffle
them all.
Instructions for preparing text
extract:
- Open the Windows Notepad. (Commands: Start /
Run / notepad ENTER). If you have a non-Windows machine, use a text
editor similar to Notepad.
- In your completed Excel spreadsheet, highlight
columns C, D, and E, using the technique that was demonstrated in class.
(Click and drag in the lettered area above the cells, not in the cells
themselves.)
- Use the Edit / Copy command (or Ctrl+C if you
prefer).
- Switch to the Notepad window.
- Use the Edit / Paste command (or Ctrl+V if you
prefer).
- In Notepad, issue the Edit / Select All command
(or Ctrl+A if you prefer).
- In Notepad, then issue the Edit / Copy command
(or Ctrl+C if you prefer).
- In your e-mail program, go into the body of a
new e-mail message and paste the Notepad text that you copied from the
previous step. If you make an attachment, you will not receive any
credit. Simply paste into the body
of an e-mail message.
- Send the e-mail to Mr. Hansen with a subject
line similar to the following:
__Spreadsheet data from Sam Student 2/15/2006.
|
|
|
F 2/17/06
|
No
school (faculty professional day).
|
|
|
M 2/20/06
|
No
school (holiday).
|
|
|
T 2/21/06
|
HW due: Read pp. 265-269 and the top of p. 270; write pp.
281-282 #2-10 even.
|
|
|
W 2/22/06
|
HW due: Write pp. 281-286 #1-11 odd, 27.
In class: Review.
|
|
|
Th 2/23/06
|
Test on
Sampling Distributions, One-Sample t
Procedures, and Confidence Intervals for a Proportion. This will cover all material through the top of p.
270.
For your studying help, here is the answer key to the 2/10 test: ABACD BBEDE CBABE.
|
|
|
F 2/24/06
|
HW due: Reconvene your group (see assignments below if you
have forgotten who your group members are). Write a revised research question and methodology for an experiment
involving blocking in some manner
and using at least 50 data points. Also include a description of the null and
alternative hypotheses you will test, or if you prefer, what parameter(s) you
hope to develop confidence intervals for.
One submission is required from each group leader. E-mail format is
preferred; however, hard copy will also be acceptable. If you send e-mail, do not send an attachment.
(Attachments will be discarded.) Instead, paste the text into the body of
your e-mail message. Remember to put a double underscore ( __ ) at the
beginning of the subject line.
Group 1: Kenny, Greg, Chris
Group 2: Andrew B., Clay, Will
Group 3: Ben, Paul, John
Group 4: Christian (newly appointed leader) and Glenn, with partial
assistance from Mr. Hansen*
Group 5: Jeffrey, Michael L., Henry
Group 6: Alex, Andrew H., Michael M.
* Group 4 will use Mr. Hansen as a partial group member to assist with
blinding, data collection, etc. However, in the manner of a true student, Mr.
Hansen will occasionally miss meetings and may be late submitting requested
inputs. Therefore, the group leader will have to have contingency plans to
make sure that the project stays on track.
Quiz during class: You will be
required to produce a correct answer when called upon to each of the
questions on yesterday’s test.
Here are the raw statistics for the test, not counting the 14-point bonus:
n = 17
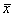 = 65 = 65
s = 17
5-number summary = 37, 50, 68, 77, 100
Because the s.d. was so large, I adjusted the scores to bring them into a more
typical domain of 49 to 100. That made the statistics as follows:
n = 17
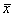 = 72 = 72
s = 14
5-number summary = 49, 60, 75, 81, 100
The 14-point bonus (added after the adjustment) brings all students to 60 (D)
or above.
|
|
|
M 2/27/06
|
HW due: Develop a timeline for your
group project. In most cases, your proposal also needs to be revised to
incorporate blocking in a more useful way.
Remember, we always block first
(before randomly assigning subjects to treatment or control groups), and we
block on some characteristic that we think would otherwise be likely to be a
lurking variable. Recall how, in the classroom example concerning the effect
of temperature on math test-taking ability, we said that it might be
advantageous to block on math ability (low/high, or low/medium/high) before
doing the random assignment. We would probably not block on height in this case, because it is quite unlikely
that height is a lurking variable of any consequence. (It could be, perhaps
at a school that recruited heavily for basketball, but not at STA.)
Regarding your timeline: Be realistic, and set goals that you are quite
certain you can meet with a safe margin. I am not expecting a final writeup
by the end of the quarter (March 10), but I am hoping that you will be
finished by the middle of the following week. If you can’t finish before
spring break (March 17), then you will have the assignment hanging over your
head for a longer period. I will accept reasonable requests for extensions,
but only if they are made in a timely fashion. For example, a sudden request
for a 2-day extension would be denied if it were made immediately before a
deadline, especially if your group still has 2 days’ worth of work left to
do. (Reason: If you still have 2 days’ worth of work to do, then you
obviously must have known there was a problem at least 2 days before the
deadline. A request made the night before is not timely. Bad news never
improves with time. Tell me early if you can foresee a problem, and we can
work something out.)
The following intermediate checkpoints
are required:
- At some time before you commence gathering
data, I need to see and approve your release form (a simple piece of
paper that your subjects will sign to acknowledge that they have been
properly informed of the protocol of the experiment and that they
consent to be part of it).
- By no later than Wednesday, March 8, I need to
see an Excel spreadsheet file of at least some of the raw data that you
have gathered. If your data gathering is still in progress, that is
acceptable, but you need to have something to show.
You will have some class
time (approximately 1 hour per week) to meet with your group members to plan
your project and work on administrative details such as release forms.
However, the data collection, analysis, and writeup will need to be done
outside of class.
Here is an example of what I am expecting from you in terms of a timeline:
M 2/27: Submit revised proposal.
T 2/28: Meet with Mr. Hansen in Math Lab to discuss possible improvements to
methodology. Also ask him about our H0,
Ha, and statistical
tests we plan to use (2-sample t?
1-sample t with matched pairs?).
W 3/1: Meet with group members to finalize methodology and recruit volunteer
subjects.
Th 3/2: Make short lunch announcement enticing test subjects (only if
convenience sample failed). Also obtain approval of release form from Mr.
Hansen.
F 3/3: Data gathering after school.
M 3/6: Data gathering (contd.)
W 3/8: Show initial batch of raw data to Mr. Hansen.
Th 3/9: Data gathering (conclusion).
M 3/13: Submit rough draft of analysis/report writeup to Mr. Hansen for
comment.
W 3/15: Work after school with group members to revise and proofread writeup
(allowing 2 days for turnaround from Mr. Hansen).
Th 3/16: Submit project report and group leader report.
Of course, this is only an example. It is unlikely that anyone’s project will
exactly match this template.
A group leader report (10 points) is required in order to give specific
reasons for the proposed division of points. Give your recommendation in
terms of percentages (e.g., 30% + 33% + 37%) and justify precisely why that
division is appropriate. Do not simply talk about your impressions of how
well everyone worked. List products, meetings missed, meetings saved,
worthwhile ideas generated, etc. The length should be 1 or 2 paragraphs. If
you omit the group leader report, I will divide points equally, except with a
10-point deduction for the group leader.
|
|
|
T 2/28/06
|
HW due: Develop an experimental design diagram, similar to
the one on p. 437 of the book, for outlining your methodology. Remember to
show the “blocking split” first, then the random division into experimental
and control groups (or parallel paths in the event of matched pairs). Write a
sentence to indicate what your raw data will consist of and the units in
which the raw data will be measured. Estimate the mean and s.d. (a ballpark
figure will suffice for now) along each pathway.
This task is probably most easily accomplished with pencil and paper.
However, if you wish to use a graphics program (e.g., Windows Paint) or a
business presentation package (e.g., PowerPoint), that is also fine. One
advantage of using a computer is that the diagram will then be something you
can modify and incorporate into your final project report without too much
more work.
|
|