|
M 1/2/06
|
No school.
|
|
|
T 1/3/06
|
Classes resume. A blank copy of your Dec. 12 test and a complete solution key are now available.
|
|
|
W 1/4/06
|
HW due:
1. Work through the blank copy of your Dec. 12
test if you have not already done so, and compare your answers with the solution key. Since you were supposed to do
this before the end of the break, and since you will need to be doing this in
preparation for Thursday’s test anyway, you may not count this time toward
your 35-minute HW target.
2. Write up a description of the Monte Carlo simulation procedure presented
in class. Recall that we were going to use randomly chosen (x, y)
ordered pairs, where both x and y are between 0 and 2, to develop an
estimate of p. You must state your steps clearly. What constitutes a trial? How is
“success” determined? How is the probability estimate going to be transformed
into an estimate of p? Do not leave anything to the imagination of the reader.
3. Use your calculator’s rand*2 feature to execute 30 iterations of the
simulation. Record your results in a table. The function of interest, which
you should remember from Algebra II, is y
= (4 – x2)0.5.
Restrict both the domain and the range to [0, 2].
4. Use the result of #3 to estimate p.
In class: Review.
|
|
|
Th 1/5/06
|
Test on Random Variables and Probability (through p.
226). Here is the solution to yesterday’s HW to help you study.
|
|
|
F 1/6/06
|
HW due:
Correct yesterday’s test to 100%, and this time,
do the bonus simulation as well. Students who do well on this HW assignment
will receive a more lenient grading of the test itself. You may work with
your classmates to compare techniques and answers, but as always, outright
copying is not permitted.
|
|
|
M 1/9/06
|
Your two most recent tests,
including the 1/5/06 test and its associated bonus corrections, are ready to
pick up in your mailbox.
|
|
|
T 1/10/06
|
Midterm Exam (Cumulative), 8:00 a.m.–10:00 a.m., Trapier
Theater. (The published master
schedule shows a different location, but we will be meeting in the
theater, where my Algebra II students are, so that I don’t have to be in two
places at once.)
Required equipment: Calculator and writing instrument, pencil preferred.
There will be 1 bonus point on the exam if you bring a spare set of batteries
for your calculator.
The exam counts as 20% of your semester grade. Most of the exams I have given
in past years were drawn from AP review materials (sample problems in
textbook and College
Board exam archive). Therefore, you can make up your own practice exam by
assembling questions from these sources and working through the problems
under time pressure. After you have
worked the problems, you should check the answer key to learn from your
mistakes.
Warning: Some students think they
can shortcut the process by reading the questions and the answers, without
actually doing the work. In most cases, this is a disastrous mistake. Until
you have subjected yourself to the time pressure of having to write out the
answers yourself, you will not really be testing yourself. Consider, for
example, the Jan. 5 test: 3 relatively
straightforward questions totaling 39 minutes by AP timing standards.
However, most people were still writing after 50 minutes. Practice, practice,
practice. Just as you would not compete in a track meet without having
carefully practiced each of your events, you should not take an exam without
practicing as many of the standard types of problems as you can reasonably
expect to see.
|
|
|
M
1/16/06
|
No school.
|
|
|
T
1/17/06
|
No school.
|
|
|
W
1/18/06
|
Classes resume.
|
|
|
Th 1/19/06
|
HW due:
Read this
article from Business Week and prepare
for a class discussion. You will be graded on your handwritten reading notes,
which you may use during the discussion, as well as the quality and
insightfulness of your participation.
|
|
|
F 1/20/06
|
HW due:
Read this
article from Wednesday’s Post.
There will be a quiz on the article (handwritten notes permitted).
|
|
|
M 1/23/06
|
HW due: This
is a previously announced standing reading assignment. Remember that you are
responsible for the two most recent Unconventional Wisdom articles (Jan.
1 and Jan.
15). Warning: Now that we are
in the second semester, a mere passing acquaintance with the contents may no
longer be sufficient to earn you a perfect score on the quizzes. You will be
expected to provide thoughtful answers, using your powers of critical
thinking and knowledge of statistics to address the questions posed.
As with all reading assignments, reading notes are required for full credit.
There will be one or two quizzes and a discussion. You may use your
handwritten reading notes during the quiz or quizzes.
|
|
|
T 1/24/06
|
HW due:
Read pp. 239-245.
Bonus opportunity: Try solving any
of the Mathcross puzzles other than the
ones for which solutions have already been circulated. I will award a 5-point
bonus for the first completely correct solution received for each puzzle
(limit one per student).
|
|
|
W 1/25/06
|
HW due: Read pp. 245-247. Do not memorize the formulas. In fact, a much better use of your
reading note time than writing the formulas themselves would be to write, in
words, what the formulas mean, and to record the assumptions that accompany
them. Remember, you will always have the formulas themselves available for
reference during quizzes and tests.
|
|
|
Th 1/26/06
|
HW due: Compute the probability of a full house on the
draw, in 5-card draw poker. A full house is 3 cards of one value and 2 of a
different value, e.g., 3 kings and 2 nines. Show your work.
In class: Guest speaker from the College Board, Mr. Steve Graff.
|
|
|
F 1/27/06
|
Quiz (10 pts.) on yesterday’s guest
lecture. Notes are permitted.
HW due: Answer the following
question.
1. In 5-card draw poker, with no wild cards, the hands that have value are as
follows: pair, two pair, three of a kind, straight, flush, full house, four
of a kind, and straight flush (where “royal flush” refers to the highest
possible straight flush, since the cards are 10, J, Q, K, A). Any hand that
does not meet one of these criteria is called “high card” since the high card
determines the victor. (The popular name for “high card” is “junk.”)
Carefully explain the error(s) in the following calculation of the
probability of junk:
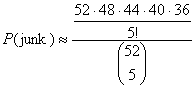
Explanation: Denominator is 52C5
as usual. Numerator is formed by avoiding any pairs. There are 52 cards
possible for the first card, 48 for the second (since pairs must be avoided),
44 for the third, and so on. We divide by 5! because the 5! = 120
permutations of the 5 cards drawn are not considered to be different hands.
Where are the mistakes, or is this analysis correct?
|
|
|
M 1/30/06
|
No
additional HW due. I will simply re-scan some of the older assignments that
some people have not done yet. (See archives to get caught up over the
weekend.)
In class: Graded discussion on last Thursday’s guest lecture. If you were not
there, be sure you have received a thorough briefing and/or notes from
someone who was.
|
|
|
T 1/31/06
|
HW due: Read pp. 226-229; write pp. 232-233 #12-17 all,
showing your work, plus the following question:
18. I have a coin that is biased to produce heads 55% of the time. If I were
to flip this coin 1 million times, what is the probability that I would
obtain at least 549,000 heads? Show work.
|
|