|
Th 12/1/05
|
HW due:
Prove, by means of simulations, that your answers to Monty Hall problem and the drawers problems are correct. I gave these
problems to you precisely because answers by analytic methods are often
wrong. In setting up your simulations, you must carefully describe the
following:
- How many digits you will select at a time from
the random digit table
- What each outcome represents
- What you will do with repeated values or
invalid values
- How you will record success or failure
- How many times (n) you will repeat the entire process
- A clear table in which you record the results
of your simulation, including the raw random digits chosen
- Tally of successes and failures
- An estimate of the true probability, showing
work as the number of successes divided by the number of trials (n).
1. In the Monty Hall problem,
use a simulation to estimate P(your
original door is the winning door).
2. In the first drawer problem, use a simulation to estimate P(other coin is gold | first coin is
gold).
3. In the second drawer problem, use a simulation to estimate P(other coin is gold | first coin is
gold).
Metaknowledge: For each of the
three simulations and associated answers, write a sentence to describe how
confident you are in the correctness of your procedure. For example, you may
write, “I think I captured the Monty Hall problem correctly, but the
probability estimate does not seem reasonable. Perhaps I need to use n > 25 next time.” Or, if you
cannot figure out how to make a table, and you are too tired to call a
classmate or send me an e-mail, you could write, “I don’t know how to make a
table that shows the results of the simulation. I thought of doing something
simple, making headings like
Trial # Random digits Interpretation Success (S) or failure (F)
—but it couldn’t really be that simple, is it?” (Actually, it is.)
You may work with your friends, but you may not copy. It is easy for me to
detect copying on an assignment like this, since the probability that two
students would have the same sequence of random digits is tiny. (The
probability of Type I error in this situation is so low that the Honor
Council would have no trouble finding guilt.)
Then, answer the following question:
4. How does Mr. Hansen estimate attendance-taking errors by lunch table
masters? In other words, how is it possible to determine which table masters
are most accurate in taking attendance without actually auditing the daily
data as the sheets are collected (which is impractical, since lunch is so
short)? Try to use the word noise
in your answer.
|
|
|
F 12/2/05
|
HW due:
Continue your work from yesterday and read this article
(only to the point where the comments begin).
Regular class, regular Friday time (9:45–10:25), regular location. I expect
legitimate answers to #1-4 from yesterday, with a minimum of 70 minutes of
time on task. “I don’t understand” from Wednesday night does not qualify for
half credit.
|
|
|
M 12/5/05
|
HW due: In
addition to your standing assignment from the Outlook section, I would like
you to read this
article concerning the education of males so that we can discuss it in
class.
|
|
|
T 12/6/05
|
HW due:
Read pp. 176-180. Also, if you have not already completed questions 1-4 from last
week (see 12/1 calendar entry), be sure to have those ready for a more
thorough grading than they received last week, when almost nobody had done
them.
|
|
|
W 12/7/05
|
HW due: Answer
the following questions on pp. 181-191: #1-4 all, 6-8 all, 10, 12-16 all, 22,
24-31 all. For each question, provide a written explanation of what formula
or technique you are using. Note:
This information is usually not provided in the answer key. You will actually
have to think about what you are doing. Problems #1 and #12 have been done
for you below as examples, leaving 20 questions. At AP pace, that is 45
minutes’ worth of work. I would like you to do all the assigned problems.
However, if you are pinched for time, I will accept a subset of 15 (approx.
35 minutes). Some of the book’s answers are debatable, and I would also like
you to flag those that you believe are shaky.
WARNING:
No credit will be given for answers that are lacking formula or technique
identification. If you parrot the book’s answer key, which usually does not
identify the source of the formula, you are learning essentially nothing.
Look at how the formulas are identified in the worked examples below.
1. Formulas for binomial r.v.:
namely, the B(25, .73)
distribution, which means n = 25, p = .73. Therefore, mX = np =
25(.73) = 18.25, and sX = Ö(npq) = Ö(25 · .73 · .27) = 2.220. However, since the
requirements for a binomial distribution are probably not met, a strong
argument can be made for choice E (“none of the above”).
12. Conditional prob. formula:
P(famine | plague) = P(famine Ù plague)/P(plague)
= .15/.39 = .385.
|
|
|
Th 12/8/05
|
HW due: pp.
181-191 #37, 39, 43-50 all. That is 10 questions, and you should be able to
complete them in 35 minutes. AP pace is 2¼ minutes each, or 22½ minutes for
all 10. That leaves you a generous amount of time to write your identifiers
and show your work. Since you have a test coming up next week, you should
also finish up any gaps (such as missing identifiers, hint, hint) in the
previous assignment.
Do all 10 questions. Extra-time students, use extra time as needed to finish
all 10 questions. Same ground rules apply as yesterday: You must identify
the formula or technique used in each case. See the examples from yesterday,
paying special attention to the parts in boldface. Believe it or not, more
than half of the students forgot to write identifiers such as “binomial r.v.
formulas” or “conditional prob. formula” when writing up their answers.
There is an educational purpose for this requirement. Using nouns to refer to
the “tools of our statistical trade” is a way of organizing our thoughts.
Just as a carpenter would say, “Hand me that screwdriver” instead of “Hand me
that thingamajig,” we should know how to refer to formulas and techniques by
name. Language guides thought. Clear-headed thinking, especially about
something as complicated as statistics, requires clear language.
|
|
|
F 12/9/05
|
No school (snow day).
HW due: Continue studying for test, even though there is no school today.
By now, I expect you to have finished all 30 of the multiple-choice problems that
were assigned. Note that your book also includes examples of free-response
problems. These are good examples of problems that you may expect to see on
Monday’s test.
In class today, we were going to continue our test review by working a
complete simulation example. Since you missed out on that educational
experience, I will reproduce it for you below.
Problem: Use a simulation
to estimate the probability that when random numbers from 201 through 300 are
selected, a multiple of 3 occurs before a multiple of 4.
Solution: [Note: Your
writeup must include the numbered instructions. In fact, writing out the
instructions is generally the hardest part of a problem like this. You must
practice doing this, or otherwise at test time you will not know how to proceed.]
1. Select digits from the random digit table, 2 at a time, where 01-99 denote
201 through 299, and 00 denotes 300. Work left to right, top to bottom,
without ever repeating any lines.
2. Treat the following as being multiples of 3: 01, 04, 07, 10, 13, 16, 19,
22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 67, 70, 73, 76,
79, 82, 85, 88, 91, 94, 97, and 00.
3. The multiples of 4 are the same as the multiples of 4 would normally be,
namely 00, 04, 08, etc.
4. Start with row 2 of the random digit table. A trial consists of drawing
numbers until either a multiple of 3 or a multiple of 4 is obtained.
5. For each trial where a multiple of 3 occurs strictly before a multiple of
4, record “success.” If a multiple of 4 occurs first, or if a multiple of 3
and a multiple of 4 occur together (04, 16, 28, etc.), record “failure.”
6. Perform a total of 15 trials.
7. Calculate probability estimate as the number of successes divided by 15.
|
|
|
|
Trial #
|
Random digits
|
Interpretation
|
Success
|
Failure
|
|
|
|
1
|
59 88
|
mult. of both 4 and 3
|
|
ü
|
|
|
|
2
|
43
|
mult. of 3
|
ü
|
|
|
|
|
3
|
11 80
|
mult. of 4
|
|
ü
|
|
|
|
4
|
53 11 58
|
mult. of 3
|
ü
|
|
|
|
|
5
|
44
|
mult. of 4
|
|
ü
|
|
|
|
6
|
69 94
|
mult. of 3
|
ü
|
|
|
|
|
7
|
86 85
|
mult. of 3
|
ü
|
|
|
|
|
8
|
79
|
mult. of 3
|
ü
|
|
|
|
|
9
|
67
|
mult. of 3
|
ü
|
|
|
|
|
10
|
05 81 18 45 14 75 01
|
mult. of 3
|
ü
|
|
|
|
|
11
|
11 30 06 63 39 55
|
mult. of 3
|
ü
|
|
|
|
|
12
|
50 41 15 86 60
|
mult. of 4
|
|
ü
|
|
|
|
13
|
65 89 13
|
mult. of 3
|
ü
|
|
|
|
|
14
|
11 97
|
mult. of 3
|
ü
|
|
|
|
|
15
|
10
|
mult. of 3
|
ü
|
|
|
|
|
Trial #
|
Random digits
|
Interpretation
|
Success
|
Failure
|
|
|
|
Final answer: estimate = sample proportion =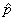 = 11/15 = .733. = 11/15 = .733.
|
|
|
M 12/12/05
|
Test on probability,
including symbolic logic, random variables, LOLN, Type I and Type II error,
PPV, and simulations. There are no tests
from previous years that combine all of these topics into a single test, but
if you prowl through the archives, you can find examples of most of these.
The notable exception is symbolic logic, which is why I am providing the
following worked examples to help you review:
Problem: Simplify (A Ù ~(B Þ ~(B Ú ~A)))
and use a truth table to prove equivalence to your simplified version.
Solution: Work from the innermost parentheses outward. Your
five tools are the following:
DeMorgan’s Laws: ~(P Ù Q) Û ~P Ú ~Q, and
similarly, ~(P Ú Q) Û ~P Ù ~Q
Definition of Implication: (P Þ Q) Û (~P Ú Q)
Distributive Law for AND over OR: P
Ù (Q Ú R) Û (P Ù Q) Ú (P Ù R)
Distributive Law for OR over AND: P
Ú (Q Ù R) Û (P Ú Q) Ù (P Ú R)
Start with ~(B Ú ~A), which
becomes ~B Ù A.
Therefore, the portion (B Þ ~(B Ú ~A))
can be rewritten, by the substitution principle, as (B Þ (~B Ù A)). By the definition of implication, this becomes (~B Ú (~B Ù A)).
Here you have to use some common-sense reasoning. What does it mean to say,
“~B or (~B Ù A)”? If A is true, the
statement will be true iff ~B is
true. Moreover, if A is false, the
statement will be true iff ~B is
true. In other words, A plays no
role here, and the portion (B Þ ~(B Ú ~A))
can be rewritten simply as ~B.
Working outward to the next level, we have ~(B Þ ~(B Ú ~A)),
which simplifies to ~(~B), or
simply B.
Whew! That means that our original statement is equivalent to A Ù B. Now we need a truth
table to prove equivalence.
Proof of Equivalence:
|
|
|
|
A
|
B
|
~A
|
B Ú ~A
|
~(B Ú ~A)
|
B Þ col. 5
|
~(col. 6)
|
A Ù ~(col. 6)
|
A Ù B
|
|
|
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
|
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
|
|
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
|
|
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
|
|
|
Since the last two columns have an identical pattern for all possible values
of A and B, the final two columns must be equivalent expressions. (Q.E.D.)
Would you be asked to do something that difficult on a real test? No,
probably not, since time is so limited. However, if you were provided some of
the proof, you should be able to fill in the holes.
If you were asked to do an entire problem (i.e., not just as a fill-in), here
is an example of the level of difficulty you should be able to handle:
Problem: Simplify ~(~A Þ ~B) and use a truth table to
prove equivalence to your simplified version.
Solution: By the def. of implication, ~A Þ ~B
means that the “if” part, namely ~A,
is false, or the “then” part, namely ~B,
is true. That means that ~A Þ ~B is equivalent to A Ú ~B. Taking the negation of
this, we have ~(A Ú ~B) Û ~A Ù B by
DeMorgan’s Law. Final answer: ~A
Ù B.
Alternate Solution: From geometry, you should remember that (~A Þ ~B) is
equivalent to (B Þ A),
which by def. of implication is equivalent to (~B Ú A). Taking the negation of this, we have ~(~B Ú A) Û B Ù ~A by DeMorgan’s Law. Final answer: B Ù ~A, which is the same as
before.
Proof of Equivalence:
|
|
|
|
A
|
B
|
~A
|
~B
|
~A Þ ~B
|
~(~A Þ ~B)
|
B Ù ~A
|
|
|
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
|
|
|
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
|
|
|
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
|
|
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
|
|
|
|
Since the last two columns have an identical pattern for all possible values
of A and B, the final two columns must be equivalent expressions. (Q.E.D.)
|
|
|
T 12/13/05
|
Makeup Test, 7:00 a.m., Room R. The five (5) students who missed school yesterday
should all plan on being there.
HW due: Each of the following is a
“testing situation” that involves some possibility of Type I and Type II
error. For each scenario, state (a) what the null hypothesis is in this
context, (b) what constitutes a Type I error, (c) what constitutes a Type II
error, and (d) which is more important to minimize, the probability of Type I
error or the probability of Type II error.
1. A grand jury is attempting to determine whether the evidence against an
alleged criminal is strong enough to return an indictment.
2. A court of law is attempting to test whether the evidence against an
alleged criminal is strong enough to warrant a conviction.
3. A car alarm microprocessor is attempting to determine whether the
jostlings it is detecting are unusual enough to warrant sounding the alarm.
4. A pharmaceutical manufacturer is attempting to determine whether
occasional adverse health outcomes among test subjects are a statistical
“fluke” or evidence of a real safety problem with the medication.
|
|
|
W 12/14/05
|
HW due:
Read pp. 205-211; write pp. 212-213 #5, 8. Please show some work of your own.
(Even if it is somewhat cryptic, that is better than merely copying the
book’s explanation.)
|
|
|
Th 12/15/05
|
HW due:
Write pp. 211-214 #1-12 all. If you did #5 and #8 previously, you do not need
to do them again. Note that completion is expected, since AP pace is 2¼
minutes per problem. Even extended-timers are expected to complete all 10
problems. Show some work for each problem. Another NOPQ (Notebook-Open Pop
Quiz) is possible. (Hint: It is
therefore to your advantage to show enough work to help you learn. If you
merely “pencil-whip” the problem, you probably won’t be very well prepared.)
|
|
|
F 12/16/05
|
HW due:
Read pp. 217-226. This is essentially all review and should be easy and
quick, even though you have Lessons and Carols taking time away from your
study time on Thursday night.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|