|
M 10/3/05
|
HW due:
Make sure that last Friday’s HW is complete. If not, then devote another 35 minutes.
If it is complete, then remember that you have your group project to work on.
Warning: Anyone who does not have
lists SALES and ADCST displayed in STAT EDIT mode (due Thursday 9/29) will
not earn full credit on today’s HW check. You may need to recreate those
lists if they were destroyed by another operation. Even if they were not
destroyed, you may need to ask a classmate to show you how to add them to the
STAT EDIT display so that they are shown as vertical lists. (I tried to show
as many people as possible on Friday, but a few escaped before I could
finish. The secret is the 2nd LIST menu.)
|
|
|
T 10/4/05
|
HW due:
Read pp. 78-80. Also, for the several people who still did not have lists SALES
and ADCST displayed in STAT EDIT mode yesterday, this will be checked yet
again today (an easy 4 points for those who earned the points yesterday).
|
|
|
W 10/5/05
|
HW due: First,
send me an e-mail with subject line beginning with double underscore (__) so
that I can recognize the message as being non-spam. State your name, and send
the message from the e-mail address that you check most frequently. IMPORTANT: STATE YOUR NAME. NO CREDIT
WILL BE AWARDED FOR MESSAGES THAT ARRIVE WITH NO NAME. I will respond
with data entry instructions. As you perform the data entry, you will need to
make your best judgment concerning how the student would have entered the
data if a computer had been provided.
Update as of 5:00 p.m.: I have received a grand total of two (2) e-mail
addresses out of the 18 that I was expecting. So . . . below the dashed line
are the instructions from Mr. Baad. Note:
Sending me the e-mail message is still required as part of your HW
assignment. When you have finished, send me a second e-mail with the serial
numbers (found on top of first page) for the survey forms that you entered.
[Forwarded message from Mr. Baad follows.]
====================================
http://www.zoomerang.com/survey.zgi?p=WEB224LLTT6G44
Here is the link. I’d like the boys to type in the text from the written answers
as well as just clicking on the bubbles. There are about 15 surveys on which
boys wrote comments on the back of the last page. If a boy gets one of those,
make sure he types the comments in the box that is provided for question #30.
Thanks again for your help.
|
|
|
Th 10/6/05
|
HW due:
Work as many problems as you can on pp. 81-89. Note the following
instructions.
1. Each time you get a problem correct, show your work. If there is no work
to show, then write a suggested modification to the problem so that it would
be more challenging.
2. Each time you get a problem incorrect, write a sentence explaining why you
made the mistake you did and what (if anything) you have learned as a result.
3. All written work must be shown on a standard homework paper, not in the
margin of your book.
|
|
|
F 10/7/05
|
No school.
|
|
|
M 10/10/05
|
No school.
|
|
|
T 10/11/05
|
No additional HW due. You
have your group project to work on, and you should be sure you are fully caught
up on existing HW. Also, although we were hobbled last Thursday by the
unexpected absence of 39% (!) of the class, some worthwhile things were
discussed, such as the Rule of 72. You
are responsible, as always, for everything covered.
|
|
|
W 10/12/05
|
HW due: Group Project #1. Extensions are possible by
special permission. Please note, last-minute extensions are generally not granted.
(Reason: This is as good as an admission that you did not start working
seriously until the last minute. If you had started earlier, you would have
realized earlier that you needed to request an extension.)
|
|
|
Th 10/13/05
|
HW due: Send
me an e-mail describing exactly what you did, or thought you did, during last
week’s survey data entry. For example, where did you click on the “Submit”
button? If you intentionally did
not actually enter the forms whose serial numbers you gave me, state that.
(Obviously, accidental omissions mean that you need to re-enter the data, but
that is not an honor code violation.)
IMPORTANT: Please also comment on
whether you think the following proposed combination of penalties for the
students who confess to “pulling a Newman” would be too harsh, too lenient,
or about right:
- Zero on the homework
- Zero on yesterday’s quiz (since, clearly, the
answers were fanciful)
- Both zeros undroppable
- Additional 10-point penalty for the
inconvenience and waste of time caused for Mr. Hansen and Mr. Baad
- Must re-do data entry correctly for no points
- Overall effect will be approximately half a
letter grade lower on the quarter grade
- No visit to the Honor Council
|
|
|
F 10/14/05
|
Big Quiz (60 pts.) on correlation, regression, residual plots, and curve fitting. This
quiz will be quite similar to the Oct.
2000 Big Quiz. An answer key
is available, but if you check the answer key before first attempting the
problems, I will reach out through cyberspace and smite you with a reprimand.
You may also find the LSRL handout
to be informative. It is a likely treasure trove of quiz questions.
|
|
|
M 10/17/05
|
HW due:
Write #3 on p. 101 and the programmed
learning exercise. A solution is provided to the p.101 problem, but you
should answer the question on your own, comparing only at the end.
|
|
|
T 10/18/05
|
Form VI retreat (no class).
|
|
|
W 10/19/05
|
HW due:
Consider the data set below and answer the questions that follow.
{(1, 5), (2, 6.1), (3, 8), (4.2, 9.5), (7, 12), (8, 13), (8.2, 13.5), (9,
16), (10, 19), (12, 22)}
1. Prove that the LSRL fit is inappropriate despite the high r value. What value for r did you get?
2. One possibility is that X and Y are related by an exponential
function. If this is so, what function do you need to apply to Y so that a transformation to achieve
linearity can occur?
3. Apply the transformation (i.e., inverse function) to Y and perform a LSRL fit between X and the transformed Y.
Write your results: log y » ________________ + ________________ x
4. Use precal techniques to solve the equation in #5 for y.
5. Perform STAT CALC 0 on your calculator to prove that your calculator can
do the same thing as you just did, only faster.
6. In #5, what do the r and r2 values represent?
___________________________________
7. Another possibility, besides exponential, is that X and Y are related by
a power function, i.e., a function of the form y » axb where a and b are unknown constants. If this is true, then what do we get
after taking the logarithm of both sides? (Simplify the equation, using
precal techniques.)
8. If #7 is true, is it obvious to you that log y must be a linear function of log x? ________
9. Perform a LSRL fit with log x as
explanatory variable and log y as
response.
10. Summarize what you know: log y » ________________ + ________________ log x, where ________________ plays the
role of log a and ________________
plays the role of b.
11. Use precal techniques on the results of #10 to obtain a power-function
mathematical model for y, i.e., an
equation in the form yhat = axb.
12. Perform STAT CALC A on your calculator to prove that your calculator can
do the same thing as you just did, only faster.
13. Which is the best model for the given data set: linear, exponential, or
power? Why?
|
|
|
Th 10/20/05
|
HW due:
Make sure yesterday’s assignment is ready to hand in, and add a paragraph
(several sentences) of comment regarding our upcoming project to survey the
dietary habits of STA students.
|
|
|
F 10/21/05
|
HW due:
Read pp. 103-109.
|
|
|
M 10/24/05
|
HW due:
1. Explain Simpson’s paradox in your own words (approximately one paragraph).
If possible, try to teach the paradox to a sibling who is old enough to
understand percentages, or to a parent.
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2. Then write a second paragraph explaining why the baseball statistics (see
table below) illustrate Simpson’s paradox.
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
3. What is the lurking variable for the batters named Ahnold and Bloke?
____________________
4. Are the numbers in the BA columns correct? ______
5. Every pitcher is either right-handed or left-handed. Since Ahnold is a
better batter than Bloke when facing right-handed pitchers, and a better batter than Bloke when
facing left-handed pitchers, it seems logical that Ahnold must be a better
batter than Bloke. How can it be that Bloke is better overall?
____________________________________________________________________
____________________________________________________________________
6. Consider two new batters named Cad and Dustbin. Let CR and CL
denote the batting averages for Cad when facing right-handed and left-handed
pitchers, respectively. Let DR
and DL denote the
batting averages for Dustbin when facing right-handed and left-handed
pitchers, respectively. Invent 4 3-digit decimal values for CR, CL, DR,
and DL, none of them
ending in zero, such that CR
> DR and CL > DL, but in such a way that
no amount of fiddling with the lurking variable you identified in #3 could
ever cause Dustbin’s overall batting average to be higher than Cad’s. In
other words, invent 4 values that make the data “paradox-proof” against
Simpson’s paradox. No work is needed. List your 4 values here:
CR =
__________ CL
= __________ DR
= __________ DL
= __________
|
|
|
|
|
Ahnold
|
|
|
Bloke
|
|
|
|
|
|
|
H
|
AB
|
BA
|
H
|
AB
|
BA
|
|
|
|
RH pitchers
|
112
|
400
|
.280
|
162
|
600
|
.270
|
|
|
|
LH pitchers
|
150
|
600
|
.250
|
36
|
150
|
.240
|
|
|
|
Total
|
262
|
1000
|
.262
|
198
|
750
|
.264
|
|
|
|
Note for those who did not grow up reading baseball
statistics: H = hits, AB = at-bats
(i.e., number of trips to the plate, not counting walks or getting on base by
being beaned), and BA = batting average. BA is defined as H/AB, expressed as
a 3-place decimal.
|
|
|
T 10/25/05
|
HW due:
Read pp. 121-122, and work all the way through the example in tomorrow’s
calendar entry.
In class: Review day. There will be a Quick
Quiz (graded and returned immediately) on bivariate data to see if you are
on your toes. Two-way tables, Simpson’s paradox, and methods of data
collection may be included.
|
|
|
W 10/26/05
|
No additional HW due today.
This is your chance to get caught up on old HW. There may be an audit of past
assignments today.
In class: Review.
|
|
|
Studying for the test (evening of 10/26)
|
The Big Quiz will be
available for pickup Wednesday afternoon in the Math Lab beginning at about
3:00 p.m. For those who cannot make it and would like to have a good practice
review, here are a blank copy and an answer key that you can use to challenge
yourself.
Note: You should be able to
complete the entire Big Quiz in 10-15 minutes (about 20 minutes for extended
time). You might want to take it a second time to see if you can improve your
speed and proficiency.
|
|
|
Th 10/27/05
|
Test on Bivariate Data, Including Two-Way Tables,
Simpson’s Paradox, and Methods of Data Collection. For multiple-choice questions involving simple
transformations to achieve linearity, you are allowed simply to punch buttons
on your calculator (e.g., ExpReg or PwrReg). However, for free-response
questions, you may be asked to show the derivation of the mathematical model.
Here is a completely worked example:
Consider the following data set:
{(375, .1), (425, .21), (480, .4), (510, .51), (560, .7), (630, .88), (700,
.97), (770, .995)}
Make a scatterplot. The relationship is the S-shaped curve we learned about in class. The official name is ogive (pronounced O-JIVE), and in fact
you may already recognize this as being the cumulative normal distribution
for a typical SAT Math test. [The calculator notation for this is normalcdf,
but you are not allowed to write calculator notation except on scratch paper.
If you accidentally write normalcdf somewhere on your test paper, make an “X”
through it so that it will be ignored during grading.]
Next step: Transform Y by applying
the inverse of the supposed relationship. The inverse of the cumulative
normal distribution is called the inverse normal. Therefore, let f represent the cumulative standard
normal distribution (m = 0, s = 1), and let f –1
represent the inverse normal. [Note to student: You cannot write invNorm on
your paper, since that is considered to be “calculator notation.” Points are
deducted on the AP if you write words like normalcdf or invNorm.]
Let y = g(x) represent the
“true” relationship between X and Y. Since we think g is a cumulative normal distribution for some unknown values of m and s, we apply f
–1(Y) to produce a new
list that should, hopefully, be linearly related to X.
Perform a LSRL fit between X and f –1(Y). [Do it!] The LSRL model has extremely strong linear
correlation (r = .99996), allowing
us to say the following:
f –1(y) » –4.943. . . + .0097. . .x
The only remaining question is what we should use for m and s as we develop a model that relates the original X and Y. Plot the LSRL and note where the LSRL crosses the lines y = –1, y = 0, and y = 1.
Because these indicate z scores of
–1, 0, and 1, respectively [note to student: that’s the whole point of
invNorm, to return a z score], we
can use our calculator [2nd CALC INTERSECT] to find the crossing points, from
which we deduce
m = 507.13. . .
s = 102.796. . .
Therefore, our model is
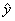 = cumulative normal
distribution with m = 507.130, s = 102.796.
[It would certainly be more efficient to write 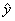=normalcdf(–99999,x,507.130,102.796), but alas, that is
not allowed.]
Now, make a residual plot. [Calculator steps: Y= key, Y1=normalcdf(–99999,x,507.130,102.796) 2nd QUIT Y1(L1)®L4 ENTER to create an L4 column that
contains 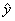values for each x value. Then, press
L2–L4®L5 ENTER to store all the values of y – 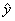, i.e., the residuals, into L5. Finally, set up
a scatterplot of L1 versus L5 and press ZOOM 9.] The
residual plot is suitably random, telling us that our cumulative normal
distribution with the m and s values that we found would be an appropriate fit.
|
|
|
F 10/28/05
|
Make-up test, 7:00 a.m., Room R.
In class: No additional HW due, but some old HW may be checked or re-checked.
Of course, a quiz on last Sunday’s “Unconventional Wiz” column in The Washington Post is always a
possibility. (Search www.washingtonpost.com
for Richard Morin if you forgot to read the column last week.)
The same writer, Richard Morin, also wrote a much longer article that ran on
the same day (Sunday, Oct. 23) in The
Washington Post Magazine. The subject was an opinion poll of teenagers in
the D.C. area as compared with a sample of teenagers nationwide. This article
may be worth discussing next week, but it will not be quizzed today.
|
|
|
M 10/31/05
|
HW due:
Consider the following data set.
{(50, 9490), (51, 10400), (52, 11400), (53, 12500), (54, 13700), (55, 15000),
(56, 16400), (57, 17900), (58, 19500)}
1. State the linear model that best fits these points.
2. State the r value.
3. Sketch the scatterplot (with line overlaid) and the residual plot. What
can you conclude?
4. Use the methods we learned to develop a fit from X to Y as a 7th power
of a linear function.
5. Sketch a new scatterplot (with this new curved fit overlaid) and a new
manually developed residual plot. What can you conclude?
|
|