|
W
9/7/05
|
First day of class.
|
|
|
Th
9/8/05
|
HW due:
Reading assignment on how
to study statistics. Reading notes are required (follow HW guidelines—see
link). There will also be a short Quiz
to test your knowledge of the alphabet, the attendance
policies, and the reading assignment.
|
|
|
F
9/9/05
|
HW due:
Read pp. 1-12. Reading notes are required, as always. Also work some problems
beginning on p. 13.
|
|
|
M
9/12/05
|
HW due:
Two-part assignment.
1. Make up a data set, as we did in class on Friday, except this time for a
hypothetical Ms. Denizé test. Use at least 15 data points. List all 15 on
your paper. Be sure to use a set that is unique to you. Compute the sample
size, sample mean, mode, median, sample standard deviation, range, and
5-number summary. Be sure to use correct notation for sample size, sample
mean, and sample standard deviation. (For example, that means that you cannot
write “sample size = 15”; instead, you must write “n = 15.”)
2. List a data set of people’s heights (in inches) with the following
property. The maximum height minus the Q3
height must be greater than the quantity 1.5(Q3 – Q1).
In other words,
max – Q3 > 1.5(Q3 – Q1).
Note: The quantity Q3 – Q1 is called the interquartile
range (IQR) of the data set. What is your IQR?
|
|
|
T
9/13/05
|
HW due:
Read pp. 22-31. Reading notes are required, as always (follow the homework guidelines). Note the typographical error in
the middle of p. 31: The bell curve area covering ± 3s should be 99.7%, not 99%.
|
|
|
W
9/14/05
|
HW due:
Read through p. 38, and begin working multiple-choice questions on pp. 39-46.
For each question, show your work, your initial guess, your second guess, and
finally (if it takes you several tries) the correct answer based on the
explanations beginning on p. 47. Important:
If you were not correct with your initial guess(es), you must write a
sentence of explanation for why you were initially led astray, and what you
have learned in the process. All 28 questions will eventually be required,
but for now, just do as many as you are comfortable with.
Incidentally, I will not accept a HW paper that shows nearly all of the
answers as being correct on the first try. I have enough years of experience
to know that almost nobody is that proficient with multiple-choice questions.
They are much harder than you think. Make sure to commit to an answer, and
write it down before checking the answer key.
|
|
|
Th
9/15/05
|
HW due:
Continue the problems you began yesterday. By now you should be able to do
all, or nearly all, of them. If time permits, tackle one or two of the
free-response questions as well.
|
|
|
F
9/16/05
|
HW due:
Fill out as much of the Sept. 2000
test as you have time to do, including Part V (preview of coming
attractions). Ignore the question about Chebyshev’s Theorem. The answers to
Part V are as follows:
21. positively
22. response, r
23(a) r » –1 (b) r » –0.8
A normal quantile plot (#14),
sometimes called a normal probability plot, is not an AP topic. However, as
we shall see, it is an extremely useful tool for checking for normality or
skewness. Basically, the NQP has data values (xi) on the horizontal axis and z scores on the vertical axis.
The notation N(whatever, whatever),
mentioned in the instructions for problems #16-20 on the test, means a normal distribution whose mean is the
first number and whose standard deviation is the second number.
For your own benefit, please also do as many of the problems on pp. 39-49 of
the Barron’s book as you can, including free-response questions #1-3 on p.
49. If you cannot do all these for today, then do them over the weekend.
In class: Review and technology demonstration.
|
|
|
Weekend
|
Study for test. We went
over the answers to #1-8 from the Sept.
2000 test in class. Here are the rest:
9. [Cross out “63 to 97” at the very end of the second sentence and write
“34” instead. Remember, range is a single number that equals max minus min.]
10. [Cross out “boxplot” and write “stemplot” or “histogram” instead.]
11. [Already done for you.]
12. Uniform; histogram was given in class. The bars should vary slightly in a
real-world data set. Bars are labeled 1, 2, 3, 4, 5, 6, and the vertical
scale would be labeled with the count. For example, if you did 600 rolls, the
vertical scale should be at or near 100 for each bar.
13. Skew left, with a small bump at the left for infant mortality. The left
skewness is caused by the fact that the data points are clamped at the right
end. Since virtually nobody lives beyond 110, the left tail is longer than
the right tail. Boxplot: ├───[|]─┤
Five-number summary: 0, 60, 72, 84, 113. (These numbers are made-up. I did
not get them from an actual demographic data source.)
14. Skew right, since a few multimillion-dollar houses at the high end will
dramatically raise the mean house price. Nearly all the houses are clustered
in the $400,000 to $1,000,000 zone. To see the NQP, which you should be able
to sketch after displaying on your calculator, perform the following steps:
Enter the following data set into L1:
400000
500000
600000
700000
700000
800000
10000000
50000000
200000000
Notice that the mean is $3.3 million, even though the 5-number summary is
$400K, $550K, $700K, $3M, $20M. Clearly, the median gives a truer picture of
central tendency for this skew right data set.
Punch 2nd STAT PLOT, turn Plot1 on, set Type to the sixth type (the one just
to the right of the regular boxplot and just below the histogram), set Data
List to L1, set Data Axis to X, and set the Mark to whatever you
wish. Press ZOOM 9 to display the normal quantile plot.
Do you see how the dots bend to the right? That reveals right skewness. If
the data set had been normally distributed, you would have seen a pattern of
dots in a straight line.
15.(a) IQR = Q3 – Q1 = 72.5 – 67.5 = 5 inches
(b) s = 4.734 inches
by calc.
16. 1250, 150, 1250
17. z = (x – m)/s = (1440 – 1250)/150 = 1.267
Note: You must cross your z in order to earn full credit.
18. Do a sloppy sketch like this (quickly, no more than 25 seconds):
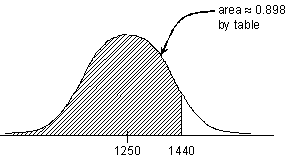
Your “work” consists of this sketch, an arrow, and the area as shown. The
table entry for z = 1.27 is shown
on p. 542. Answer: 90th percentile.
19. 45th %ile Þ z = –0.13 [by table on p.
541]
Solve equation z = (x – m)/s for x.
Show plug-ins: –0.13 = (x –
1250)/150
–19.5
= x – 1250
–19.5
= x – 1250
1230.5
= x
Answer: Bill needs a score of about 1231.
20. For 1300, z = 0.33 [no need to
show work, but do show the z
value].
For 1550, z = 2.0.
By table on p. 542, the %ile values are 62.93 and 97.72, respectively.
The area in between must be .9772 – .6293 = .348 or 34.8%.
Note: If you can manage to locate
your calculator manual, there is a shortcut you can learn about there. If you
punch in normalcdf(1300,1550,1250,150) ENTER, the calculator gives you an
answer of .347 immediately.
21-23. [See answers in 9/16 calendar entry.]
|
|
|
M
9/19/05
|
Test #1.
The test links on the main STAtistics Zone page and the “Pages from Previous Years” will give you a
good idea of the level and content to expect. Many of the questions, of
course, will be different. Under new math department policies, you will be
required to take a different test as a make-up test if you miss the test
today. The make-up test will be offered at 7:00 a.m. on Tuesday, 9/20/2005,
and is not guaranteed to be of equivalent difficulty.
Q. Mr. Hansen, if there is a
problem like #20 on the sample test, is it OK to use the normalcdf calculator
shortcut instead of all that complicated table arithmetic?
A. Yes.
Q. Does it matter that the
calculator answer to #20 was 34.7%, while the complicated table arithmetic
gave an answer of 34.8%?
A. No. This is not a math class.
The discrepancy is irrelevant, as long as you round correctly at the end. (Do
not round intermediate answers.)
Q. Do I need to write s correctly in order to receive credit
for a question involving sample standard deviation?
A. Yes.
Q. If my s looks sort of like a 5, does it count?
A. No.
Q. What if I write Sx, using the
calculator notation?
A. Sorry, not acceptable. You
could say sx (with
subscript), but s is easier.
Q. What if I confuse s and s, or xbar
and m?
A. You would lose some points. The
distinction between statistic and parameter is crucial.
Q. If you were required to
summarize the entire course in one sentence, what would you say?
A. We use statistics to estimate
parameters.
|
|
|
T
9/20/05
|
HW due:
Read p. 52 to middle of p. 66. Reading notes are required, as always.
|
|
|
W
9/21/05
|
HW due:
Write p. 367 #1-3 all, p. 370 #13, 14, 16. Do these under time pressure,
without peeking at the answers (time limit: 13½ minutes for regular students,
20 for extended timers). Save all your scratch work, sloppy though it may be.
Then, check your work against the answer key, mark each problem right or
wrong, and proceed as follows:
- For each answer that you got wrong, write a sentence
in which you describe what you learned as a result of the problem, and
locate another similar problem in the practice examinations. (Record
page number and problem number.)
- For each answer that you got right, write two or more
sentences in which you describe, in your own words, how a student should
approach the situation. Do not copy the answer from the Barron’s book or
from another student. Pretend for a moment that you are tutoring a
friend who is having trouble understanding the problem. For example, you
could explain how the various wrong choices could be ruled out.
In class: Group project
selection methodology.
|
|
|
Th
9/22/05
|
HW due:
Generate at least one written
project idea so that you have something to discuss when the groups are
convened for the first time. Also finish writing up a clean version of the
group selection methodology from yesterday’s class discussion.
If you would like to see how other classes fared with this assignment, check
out the history of old group projects.
|
|
|
F
9/23/05
|
HW due: If
you have not already done so, read “How to Study
Statistics” and be prepared for a possible quiz. Then write down 100
digits (0-9) made up from your own imagination to look like a random
sequence, plus another 100 random digits generated by using randInt(0,9)
ENTER ENTER ENTER . . . on your calculator. Do your made-up ones first, then
the calculator digits, but do not necessarily place the calculator digits
lower on the page. In other words, do not tell me which sequence is which.
(Remember for yourself, but do not tell me or identify in any way on your
homework paper which sequence is which.)
In class: First group meeting.
|
|
|
M
9/26/05
|
Class pre-empted for
assembly in Trapier Theater: Harvard University President Lawrence Summers.
|
|
|
T
9/27/05
|
HW due:
Project proposal and timeline. Spelling, grammar, and neatness count. Hard
copy is required (no e-mail submissions). On this and all other
project-related papers, all three members’ names must be on the paper, with
the group leader’s name underlined. Please see the assignment sheet for more details.
|
|
|
W
9/28/05
|
Quiz on “How to Study
Statistics” and the 9/25 Washington
Post reading (“Unconventional Wisdom” in Sunday Outlook section, p. B5).
This is probably the final reminder you will receive on the newspaper
reading, which is a recurring biweekly assignment for the entire year.
HW due: Read p. 66 through the middle of p. 70. Are reading notes
required? Yes, as always. (I will probably not remind you again.) Is working
through Example 4.6 with a calculator by your side required? Yes, as always.
The calculator commands you need (after entering the X and Y lists in L1
and L2, respectively) are as follows:
2nd QUIT [to make sure you are in the full-screen calculation entry mode, not
STAT EDIT mode]
DiagnosticOn ENTER
[This command is found on the 2nd CATALOG menu. DiagnosticOn is a one-time
command that you never need to worry about doing again unless you change the
backup battery on your calculator.]
STAT CALC 8 ENTER
Note: STAT CALC 8 is the
LinReg(a+bx) command. We do not use the STAT CALC 4 version in this class.
STAT CALC 4 is designed for students who have textbooks that refer to the
slope as a and the intercept as b. That is backwards for our purposes.
We will always treat a (sometimes
called b0) as the
intercept and b (sometimes called b1) as the slope.
|
|
|
Th
9/29/05
|
HW due:
Read through bottom of p. 74. Leave the data from Example 4.7 in your
calculator (required) so that we can go immediately to that example during
class. Use the names SALES and ADCST for your two lists (required) and Y1
for the equation of the LSRL (required).
|
|
|
F 9/30/05
|
HW due:
Read pp. 75-77 (only 3 pages) and answer the following questions.
1. Sketch two scatterplots of your own creation, each of which has an outlier
that is an influential observation (a.k.a. influential score). Circle each
influential observation. You do not need to use your calculator, but you may
if you wish.
2. Sketch two scatterplots of your own creation in which there is an
influential observation that is not
an outlier. Circle each influential observation. You do not need to use your
calculator, but you may if you wish.
3. Are the terms “regression outlier” and “influential observation” related?
If not, how can you tell them apart? Write several sentences, in your own
words, that clarify the matter as if you were explaining it to a fellow
student.
|
|
