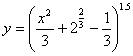AP Calculus AB / Mr. Hansen
2/22/2006

Name: _________________________

Test on Chapter 7


Time limit: 40 minutes (60 minutes for extended time)

 

Scoring

· Point values are shown in the margin.
· Most problems require only minimal work today. Follow instructions for each question.
· There is no penalty for incorrect guesses on the multiple-choice questions today.
· A calculator is allowed throughout.

 

 

1.
(10+6+
4 pts.)

Throughout the day, a population of bacteria in a dish is growing at a rate proportional to the population. At 3:00 a.m., there are 10,500 bacteria, and at 5:00 a.m., the instantaneous growth rate is 3000 bacteria/hr.

 

 

(a)

Find the particular equation expressing population P as a function of time t, where t = hours after midnight. Show minimal work.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)

Is the average rate of growth between 5:00 a.m. and 6:00 a.m. less than, greater than, or equal to 3000 bacteria/hr.? Justify your answer.

 

(c)

Show that the bacteria population first surpasses 50,000 at about 11:03 a.m.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

Given: dy/dx = ky for some nonzero constant k, and y = 0 when x = 14.

(6+4)

 

(a)

Solve the diffeq. with the initial condition given.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)

Explain why, in this case, Euler’s Method would always return exact results. In other words, explain why, for this diffeq., the Euler estimates for y are always exactly correct.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.
(8+6+
10+6+
8+6+6)

Given: . In parts (b) through (f), use the initial condition (–1, 2).

 

 

(a)

Sketch the slope field on [–4, 4] ´ [–2, 2].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)

Sketch the particular solution that passes through (–1, 2). Overlay this curve on your slope field in (a) if possible.

 

 

 

 

(c)

Show work to achieve the following particular solution: .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(d)

Compute, to 3 decimal places, the y-intercept of the true particular solution given in (c).

 

 

 

 

 

 

(e)

Use Euler’s Method (with a suitable value for Dx) to estimate the y-intercept. Work is optional, but you must state your Dx value.

Dx = __________________

 

 

(f)

Explain why (e) < (d) for everyone in the class, regardless of what value of Dx was used in (e).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(g)

Prove algebraically that all solutions in Quadrant I and II would have upward concavity.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.

Euler’s Method is a procedure for

(5 pts.)

(A) graphing slope fields

 

(B) estimating x values for a differential equation

 

(C) estimating y values for a differential equation

 

(D) finding an exact general solution for a differential equation

 

(E) finding an exact particular solution for a differential equation

 

 

5.

In general, Euler estimates for y are either too high or too low because Euler’s Method

(5 pts.)

(A) assumes that a linear approximation is valid locally

 

(B) uses too large a step size

 

(C) uses a positive step size even when a negative step size would be more appropriate

 

(D) is invalid whenever the second derivative does not exist

 

(E) was not designed to work on finite-precision calculating devices such as the
      computers of today

 

 

6.

In #5, the numerical accuracy problems with Euler’s Method can best be reduced by

(5 pts.)

(A) increasing Dx

 

(B) using real or estimated values for higher-order derivatives (i.e., Runge-Kutta methods)

 

(C) using more initial conditions

 

(D) using more lattice points in the slope field

 

(E) always separating variables and remembering to write “+C” on one side of the
      equation when antidifferentiating

 

 

7.

Say the word “EULER” aloud to me as you leave.

(5 pts.)