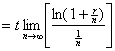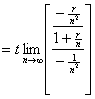AP Calculus AB / Mr. Hansen 2/2/2006

Name: _________________________

Test on Chapter 6

Time limit: 35 minutes (52.5 minutes for extended time)

Scoring	· Each numbered question is worth 12 points. Your name is worth 8 points. · Simplification is not required except for the problems requiring a numerical answer, in which case your answer must be correct to 3 decimal places. · Work is required only for problems that specifically tell you to show your work. · If you make a mistake, partial credit is possible if you show some relevant work. · A calculator is allowed throughout.
1.(a)	Compute x if
(b)	What type of problem is posed in part (a)? (The term was presented twice in class, not in the textbook.) _________________________________
2.	Given: If f is a continuous function on  (or at least on all domains involved in this problem), and if c is a constant, then . State and prove: The version of the Fundamental Theorem of Calculus that allows you to calculate a definite integral.

3.	Fill in the blanks. Abbreviations are acceptable.
	Given: Compound interest formula , where A(t) = account value at time t r = periodic interest rate n = # of compoundings per period t = # of periods P = initial deposit Prove:
	_____________________________________________________________________
	1.	| 1. Given
	2.	| 2. ____________________________
	2a.          =	| 2a. Prop. of limits
	3. Let	| 3. ____________________________
	4.	| 4. ____________________________
	5.	| 5. ____________________________
	6.	| 6. ____________________________
	7.	| 7. ____________________________
	8.	| 8. ____________________________
	9.	| 9. ____________________________
	10.          = t · r	| 10. ____________________________
	11. \ k = e^rt	| 11. ____________________________
	12.	| 12. ____________________________
		(Q.E.D.)

4.(a)	Derive a simple rule for calculating , where f is a continuous function and u is a differentiable function of x. Show your steps, but you do not need to justify each step.
(b)	= _______________________________
(c)	= _______________________________
5.(a)	Find .
(b)	Explain why L’Hôpital’s Rule is not needed in part (a).
6.	Find , showing your steps this time.
7.(a)	= _______________________________
(b)	= _______________________________
(c)	= _______________________________
8.	Compute the number of bacteria at t = 2.5 hours in a colony whose initial size is 10,000 bacteria and whose population function N(t) satisifies exponential growth with N ¢(t) = .05N(t). Units are hours and bacteria count.
	Hint: This problem is one you could have answered last year. (It is a precalculus problem, not a calculus problem.)
Bonus	What minor holiday is celebrated today?
Bonus	Explain the silly punchline to the joke regarding .