|
W 3/1/06
|
HW due:
Complete all previously assigned homework problems, and get a good night’s
sleep.
|
|
|
Th 3/2/06
|
HW due:
Check your book bag to see if you took the Chapter 7 Re-test key by accident.
Then do both of the following.
1. Determine whether you did “well” or “poorly” on Monday’s retest. (If you
did not take it, use last week’s test as your criterion.) If you did well,
write a short essay with suggestions on how your knowledge and skills can be
transmitted to the rest of the class. If you did poorly, then visit me in
Math Lab and be prepared to answer the question, “Is it me or is it you?”
2. Write §8-3 #8, 9. Remember to write a function, locate all critical
points, and then test the critical points as well as endpoints in order to
find the desired max. or min.
|
|
|
F 3/3/06
|
HW due:
§8-3 #12. Hint: Consider the right
triangle formed by the ladder and the lower left corner of the diagram. Mark
one of the acute angles as a and write a function that shows the ladder’s length as a sum of two
trigonometrically derived expressions. Then look for critical points and
proceed as with the other problems.
If you have any additional time (and you may, tonight, if you follow the
hint), please develop a separable diffeq. with solution key for sharing in
class, or work on one of the Mathcross
puzzles for extra credit.
|
|
|
M 3/6/06
|
HW due:
Read §8-4 and the material below; write §8-3 #17, 18, 20, 23 (choose any 3).
Problems 21 and 22 are also similar to past AP problems and problems I have
used on tests in previous years, but I will not require you to do them unless
you desire extra practice. Since §8-3 is one of the most practical
applications of the calculus, and one of the most difficult sections for
students to execute properly, you may be wise to do a few extra problems this
weekend for your own benefit.
What is it that students find so difficult about §8-3? In my experience,
finding the function to minimize or maximize is usually not the problem.
Instead, there are a host of common ways of losing points:
· Student ignores
constraints or forgets to use them properly.
· Student fails to write
objective function as a function of a single independent variable.
· Student forgets to
identify domain for independent variable.
· Student forgets to
check endpoints.
· Student forgets that
critical points can include DNE derivatives as well as 0 derivatives. For
example, the function 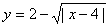 has a global max at
(4, 2), which is a cusp. has a global max at
(4, 2), which is a cusp.
· Student finds a
critical point solution but does not properly prove that it is a max or a
min. (Checking specific values to the right and left does not qualify. Algebraic sign analysis
of the expression for the derivative is usually required. Sometimes, the
second derivative test will suffice. Sometimes, you can exhaustively test all
candidates and look for the one that produces the max or min objective
function value.)
· RAWQ: Student gives a
value for x (independent variable)
as answer even though problem asked for y
or an (x, y) ordered pair.
|
|
|
T 3/7/06
|
HW due:
§8-3 #21, 22. These problems were previously assigned as optional, but now
they are required.
|
|
|
W 3/8/06
|
HW due: §8-4
#4, 8, 12, 14, 21, plus your choice of 17 or 19. If you choose #19, you will
need to do a quick bit of research to find a formula for the area of an
ellipse. (No credit for simply using the formula. Re-cast the equation of the
ellipse as two functions, y =
_______ and y = – _______ , and use
the calculus to integrate from x =
–5 to x = 5. Then compare that
result against what the formula gives you.)
|
|
|
Th 3/9/06
|
HW due:
Get a good night’s sleep and bring your previously assigned problems to completion.
Quiz: Optimization techniques and
terminology, as discussed in class. This quiz was originally planned for
Tuesday but was postponed twice because of illness.
|
|
|
F 3/10/06
|
HW due:
Read §8-5; write §8-4 #20 and the following problem:
Prove that the area of any ellipse with semimajor axis a and semiminor axis b
equals pab.
|
|
|
M 3/13/06
|
Career Day (no class for
Form VI).
|
|
|
T 3/14/06
|
HW due:
§8-5 #4, 6, 26.
|
|
|
W 3/15/06
|
HW due:
Read §8-7; write either §8-7 #Q1-Q10
(on p. 406) or §8-5 #20, 26. If you have the time, I would recommend doing
all 12 problems. However, I leave that up to your judgment.
|
|
|
Th 3/16/06
|
HW due:
pp. 427-429 #R2-R5 all, R6c, R7a.
In class: Review.
|
|
|
F 3/17/06
|
HW due: No
additional problems are required, but bring all HW for scanning. Old holes,
especially problems that we have gone over in class, are expected to be
patched now.
Quiz (10 pts., droppable) on Chapter
8, Excluding §§8-6, 8-8, 8-9. Problems to help you prepare for the quiz
can be found on pp. 431-432, #T1-T3 all, T5-T7 all. You should also finish
yesterday’s review problems if, for some reason, you were not able to finish
them on the night they were assigned.
Problem(s) on the quiz will be similar to the review problems and/or the
combined problems we did yesterday on plane areas and plane slicing. This
will not be a full-period quiz. Time limit for a problem comparable in
difficulty to what we did yesterday is 5 minutes. Arc length is included (see
examples below). The formulas for regular arc length and parametric arc
length are on the BC Calculus Cram
Sheet, since they are not an AB topic. Although you are not permitted to
use a cheat sheet during the quiz, calculators are permitted, and (as on the
AP exam) memories will not be cleared.
Sample arc length problems:
Regular: Find the length of one sinusoidal arch of the function y = sin x.
Solution: ∫0p Ö(1 + cos2 x) dx » 3.820.
Reasonableness check: A semicircle of radius p/2 would have length p2/2 » 4.935, and an inverted V passing through the points
(0, 0), (p/2, 1), and (p, 0) would have length of approx. 3.724. The
sinusoidal arc length must fall between these two values.
Parametric: Find the circumference of the ellipse x = 13 cos t, y = 12 sin t.
Solution: ∫02p Ö(169 sin2 t +
144 cos2 t) dt » 78.571.
Reasonableness check: Because the ellipse has horizontal semimajor axis of 13
and vertical semiminor axis of 12, a circle of radius 12.5 is a good approximation.
That circumference would be 25p » 78.540.
|
|
|
|
Spring break.
|
|