|
W 2/1/06
|
HW due: Write
pp. 297-301 #R1, R3, R5, R8, R9, C6.
We went over #R8b on p. 299 near the end of class. Here are all the details,
just in case you have a problem similar to this one tomorrow (hint, hint).
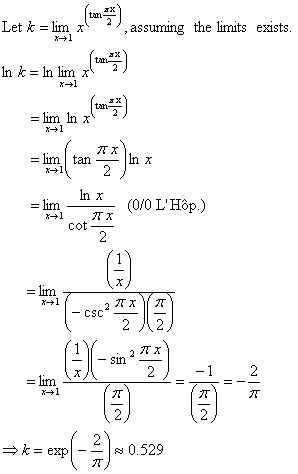
Finally, the answer to #C6 on p. 301 is “houseboat.” (Get it?)
|
|
|
Th 2/2/06
|
Test on Chapter 6. In addition to the differentiation and integration
techniques drilled (to exhaustion!) in §6-9, L’Hôpital’s Rule, and word
problems of the type demonstrated in R7e and R7f, you are responsible for the
following proofs:
1. FTC1 Û FTC2 (both
directions)
2. Chain Rule for Integrals
3. Uniqueness Theorem for Derivatives (p. 265, or the direct version that
Baird found).
|
|
|
F 2/3/06
|
HW due:
Read §7-1; write §7-1 #1-6 all.
|
|
|
M 2/6/06
|
Optional class today
(senior skip day). I will be available in my office or in Room R for those
who desire extra help.
Optional Metaknowledge HW due for extra credit: Send me an e-mail
message, timestamped no later than noon today (note: this is a 12-hour extension from what I announced in class)
in which you address each of the questions from last
Thursday’s test. Provide solutions for questions you think you missed.
However, since you can (and should) easily obtain the solutions by talking
with classmates, I am more interested in your careful analysis of why you
made the mistakes you did. If you know you answered a question correctly,
indicate that also.
Include answers to both bonus questions as well. You may confer with
classmates to obtain the answers.
Are the instructions clear? Remember, you need to list every single question,
even the ones you answered correctly. Don’t forget, as mentioned in class,
you also need to explain why FTC1 cannot be used in #1. Here is a sample of
what your e-mail should look like:
Subject line: __Sam Student’s metaknowledge!!
0. FTC1 cannot be used for #1 because ________________________ [fill in the
blank].
1.(a) I am certain I followed the correct technique. However, I realize now
that I should have done other work while waiting for the calculator to
produce the correct answer. Or, I could have performed guess-and-check with
fnInt(e^(T^2),T,1.9,2), varying the value of the left endpoint until the
answer came out to be close to 4.285. Since the integrand is positive
everywhere, I know that x<2. Since the integrand becomes huge very
quickly, I know that the solution for X is close to 2.
(b) Answered correctly.
2. FTC2-->FTC1. I accidentally provided a proof of FTC1-->FTC2. (Oops.)
Because the correct proof is found at www.modd.net/23calc/handouts/ftc1and2.htm,
I will not reproduce it here.
3. I am certain I got all of these correct except for #9, which is
L’Hôpital’s Rule. Of course, that is the most critical step in the entire
proof! I think I was baffled by the sudden use of derivatives appearing in
the problem, but of course that is exactly how L’Hôpital’s Rule works.
4.(a) CRI. I did this correctly.
(b) FTC2. I know I did this correctly, by inspection.
(c) Simple application of CRI. I know I did this correctly.
5.(a) I know I did this correctly (1, by inspection).
(b) I realize now that the form is not indeterminate, and the function is
continuous at x = 1. Since the
function is continuous, I can simply plug in the value of 1 to find the
answer.
6. I missed this, but Mr. Hansen provided the solution in class on Friday
2/3/06. My mistake was in forgetting to notice that the xth root of x is the
same as x^(1/x). [Notice how math notation can be encapsulated, crudely, in
an e-mail message.]
7. Easy--I know I got all of these correct.
8. Simple application of Pe^(rt) from precalculus. I know I answered this
correctly. I rounded the number of bacteria to the nearest integer, even
though the usual AP standard is 3 decimal places, because a non-integer
answer would make no sense in this context.
BONUS 1. ______________________ [fill in the blank]
BONUS 2. ______________________ [provide punchline and explanation]
|
|
|
T 2/7/06
|
HW due:
Read §7-2; write §7-2 #1, 9.
|
|
|
W 2/8/06
|
HW due:
Finish the assignment that was due yesterday, and add #5 or 6 (your choice).
Since there will be a HW quiz on one of these (determined randomly), you may
wish to do both to be safe. Or, if you don’t have time to write up both, you
may wish to write up one of them completely and the other in a cursory
fashion.
|
|
|
Th 2/9/06
|
HW due: Get
adequate sleep.
In class: The quiz that was originally scheduled for yesterday. This will be
based on homework and recent class discussions, with some numbers changed.
|
|
|
F 2/10/06
|
HW due: Read
all of §7-4 plus the examples in §7-3; write §7-3 #3, 4. Reading notes are
optional for §7-3. (Note: For some
reason, I had given you the wrong chapter number in the chalkboard posting.
The correct assignment is posted here on the website.)
|
|
|
M 2/13/06
|
HW due:
Write up clean versions of §7-3 #3, 4, 9. You may wish to do #9 before you
tackle #4, since the answers are given in the back of the book.
Also enter the following two programs into your calculator. Everyone must
have these before we start class on Monday. Note that you may have to hunt
around to find some of the commands (mostly under the PRGM menu) and special
characters. If you are technologically challenged, ask one of your tech-savvy
classmates to transfer the programs to you with a link cable. Whatever you
do, don’t ask an adult for help. The right-arrow symbol (→) is entered
with the STO key on your calculator, and the equal sign (=) is found under
the 2nd MATH menu. Use VARS Y-VARS Function Y1 to enter Y1.
Use 2nd CATALOG if you have trouble finding any of the other commands or
symbols. Don’t forget your editing commands (DEL, 2nd INSERT), and press
ENTER after each line. Press CLEAR to clear an entire line.
Yes, it is a bit of a challenge, but it is certainly easier than trying to
program names and numbers into your cell phone while doing several other
things at the same time, which most of you have no trouble doing.
PRGM NEW EULER2 ENTER
:ClrHome
:Disp "MR. HANSEN'S"
:Disp "IMPROVED VERSION"
:Disp "OF EULER2 1/8/05"
:Disp ""
:Disp "ENTER INITIAL"
:Disp "CONDITION AND"
:Disp "STEP SIZE:"
:Prompt X,Y,H
:Lbl AA
:Y1→S
:Y+SH→Y
:X+H→X
:Disp "NEW X="
:Disp X
:Disp "NEW ESTIMATED Y:"
:Disp Y
:Pause
:ClrHome
:Goto AA
Press 2nd QUIT to leave the programming mode. To run your program, you must
first store a diffeq. into Y1. (Y1 represents the equation for dy/dx,
in terms of x and/or y.) Then use the command PRGM EXEC and
choose EULER2 from the menu.
For the second program, please note that the expression
IS>(
refers to the name of a command found on the TI-83 2nd CATALOG menu. Also,
please note that I did not write this program; it is adapted from one at http://www.math.sunysb.edu/calculus/slope-ti85.html,
original author unknown. The only significant change is that the program
found at that site asks the user to input Xmin, Xmax, Ymin, and Ymax, whereas
the program below assumes that the user has already used the WINDOW command
to define those settings. This is a reasonable assumption and has the
advantage that rerunning the program is faster, since the user will not have
to re-enter the window settings in the program each time.
PRGM NEW SLOPES ENTER
:ClrDraw
:FnOff
:7(Xmax–Xmin)/83→H
:7(Ymax–Ymin)/55→K
:1/(.16H2)→A
:1/(.16K2)→B
:Xmin+H/2→X
:Ymin+K/2→Z
:1→I
:Lbl P
:1→J
:Z→Y
:Lbl Q
:Y1→T
:1/(A+B*T2)^.5→C
:TC→S
:X→U
:Y→V
:Line(U–C,V–S,U+C,V+S)
:V+K→Y
:IS>(J,8)
:Goto Q
:U+H→X
:IS>(I,12)
:Goto P
Press 2nd QUIT to leave the programming mode. To run your program, you must
first store a diffeq. into Y1. (Y1 represents the
equation for dy/dx, in terms of x and/or y.) Also, it
is assumed that you have used the WINDOW command to set appropriate graph
settings. Then use the command PRGM EXEC and choose SLOPES from the menu.
|
|
|
T 2/14/06
|
HW due:
Keep working on §7-3 #3, 4, 9. Send me an e-mail if you are stuck.
Also double-check your programs. Proofread them carefully to make sure there
are no typographical errors. By the way, the variables Xmin, Xmax, Ymin, and
Ymax are found under the VARS 1 menu.
Play around with your programs to see how they work. Try the following
diffeqs.:
y¢ = x
y¢ = x + y
y¢ = sin x +
cos y (define window as [–5, 5] ´ [–5, 5] before launching SLOPES program)
. . . plus any others you can think of. Be creative!
|
|
|
W 2/15/06
|
HW due:
§7-4 #2, 4.
|
|
|
Th 2/16/06
|
HW due:
Finish all previously assigned problems. Send e-mail if you are stuck. No
excuses!
If you have already finished all the previously assigned problems, then
tackle the following interesting problem:
As you know, a slope field illustrates a family of possible solution tracks.
In most cases, a small change in the position of an initial condition point
will simply move you to a nearby solution track having the same general shape
as the curve you would have been on. However, it is possible to construct
slope fields that are chaotic, or at least have a region of chaos. Try to
invent a diffeq. that produces such a slope field, and illustrate (by means
of EULER2 and SLOPES) that the situation is chaotic.
|
|
|
F 2/17/06
|
No school (faculty
professional day).
|
|
|
M 2/20/06
|
No school (holiday).
|
|
|
T 2/21/06
|
HW due:
Read §7-5; write §7-5 #1, 2, plus pp. 341-342 #R1, R2, R5. For §7-5 #2, you
will be using the EULER2 program whose listing was
provided to you previously.
|
|
|
W 2/22/06
|
Test on Chapter 7. To assist you in studying, here are solutions for
§7-4 #2, 4.
2. Sketch a grid of lattice points using window [–7, 7] ´ [–5, 5]. Then sketch stubby little segments having
slope –x/(2y) at each lattice point. You should be able to do this on your
own, without a calculator. (The AP exam requires this skill.) However, if you
have a calculator, you may use SLOPES to check your work. You should see a
family of ellipses centered at the origin. The algebraic solution is as
follows:

4a. You should have a fishhook-shaped curve that passes through the following
set of points (approximately):
{(–10, 3.1), (–9, 2.75), (–8, 2.4), (–7, 2.1), (–6, 1.85), (–5, 1.65), (–4,
1.5), (–3, 1.5), (–2, 1.5), (–1, 1.7), (0, 2), (1, 2.5), (2, 3.2), (3, 4.2),
(4, 5.5), (5, 7.2), (6, 9.4)}
Note that the curve is almost flat for x
values between –5 and –1.
b. The slope field suggests that the particular solution passing through (0,
–5) never curves back upward as x
increases, unlike the curve seen in part (a). However, proving this
algebraically is difficult. One thing you can easily notice, however, is that
the solution through (0, 2) has upward concavity everywhere, since y¢¢ = .1 + .2y¢ by the chain rule, and that is always positive in
Quadrants I and II. The solution through (0, –5) has downward concavity, at
least locally, since y¢¢ = –0.1 at (0, –5). The shape of the slope field
suggests, but does not prove, that the solution through (0, –5) never
“punches though” to reach the part of Quadrant IV where some increasing
function behavior is seen.
c. To see if there could be a solution that has no curvature, i.e., zero
concavity, compute the second derivative and set it equal to 0. By the chain
rule, y¢¢ = .1 + .2y¢, and setting this to 0 gives
.1 + .2(.1x + .2y) = 0 Þ y = –.5x – 2.5, a line with slope –.5 and y-intercept (0, –2.5). This is easy to
sketch overlaying the slope field, and indeed it seems to form a dividing
line or “ridge” between the solutions that never curve upward and the solutions
that eventually curve upward. However, since we obtained the line as a necessary consequence of setting
concavity equal to 0, we still need to verify that the line is a proper
solution of the original diffeq. Here are the steps:
Suppose y = –.5x – 2.5 is a particular solution of the diffeq. Is it true that y¢ = .1x +
.2y as required? By
differentiation, y¢ = –.5 everywhere. But as long as we stay on the
line,
.1x + .2y = .1x + .2(–.5x – 2.5) = .1x –.1x –.5 = –.5 also,
and the diffeq. is satisfied. (Q.E.D.)
|
|
|
Th 2/23/06
|
HW due:
Correct yesterday’s test to 100%. You may
consult with friends, but if you cannot explain why your answer is correct
when you are called upon to explain it, you will receive no credit. Do your
own writeup. As always, everything you write must be your own work. No
copying!
Correction to 100% is required from everybody. As a bonus, you can write a
thoughtful sentence or two (no baloney!) for each problem you missed,
explaining why you found each problem so especially difficult. Use
mathematical explanations, not “feeling” statements. Put these metaknowledge
statements on a separate sheet of paper
in order to earn the bonus.
|
|
|
F 2/24/06
|
HW due: Read
§8-2. (There is nothing to do in §8-1 except for a few simple problems that
we will go over together in class.)
|
|
|
M 2/27/06
|
Optional Re-Test on
Chapter 7, Room R, 7:10–7:45 a.m. Extra time, start at 7:05. Problems will be similar in spirit to those from last
week, though obviously not identical. If you do worse on this test than you
did on the original, your original score will stand. The 4 bonus points from
the first test are yours to keep regardless.
Double HW due: Write §8-2 #14-20 even, 21, 22. Also, be creative and
prepare a diagram similar to Figure 8-2n on p. 360. Make it complicated, and
prepare an answer key. At the start of class Monday, you will swap diagrams
with a randomly chosen classmate and will critique each other’s work. Both
assignments will be graded for completion, not accuracy. The point is to
stumble, make a few mistakes, and then learn from them.
In class: Go over the test. Just as on the real AP exam, the point breakdown
within questions is not disclosed in advance. There are no fractional points.
The score (out of 18) is multiplied by 100/18 and then adjusted by a linear
transformation (TBA). There are no fractional points in the scoring out of
18. The scoring rubric will be as follows:
1. Scoring breakdown: 1+2+2+4
(a) 1 point for saying, “Exponential growth/decay occurs if and only if the
rate of change is directly
proportional to the amount present,” or similar words.
(b) 2 points for dy/dt = k/y; –1 point if dx is used instead of dt; –1 point if RHS = 1/y; –2 points if y is not in denominator of RHS (e.g., if student has dy/dt
= ky or dy/dt = k/t)
(c) 2 points for slope field with axes and approximately 110 stubby segments
showing a family of “C” curves; –1 point if there are any stubs sketched on
the x-axis itself; –1 point if axes
are missing; no penalty for omitting lower half of sketch, since original
wording implied that y > 0 was a
requirement
(d) Student must use a differential equation involving y and t (or y and x) in order to earn any points at all. A wrong answer from (b) is
acceptable for ECF credit. Points are then awarded as follows: 1 point for
separating variables, 1 point for writing “+ C” in the antidifferentiation step, 1 point for
acknowledging/utilizing both initial conditions, and 1 point for a final function (not a relation with ±) that is consistent with student’s earlier work.
2. Scoring breakdown: 3+2+2+2
(a) 1 point for correct work supporting f
(0.5), 1 point for consistent (not necessarily correct) work supporting f (1.0), and 1 point for a correct
final answer (–3.5 or unsimplified equivalent); final point cannot be earned
by ECF
(b) 1 point for saying f (x) = –x2 – 3 (no partial credit); 1 point for testing both
properties in a coherent manner; second point can be earned via ECF if
student shows that his function fails, but not if student approves an invalid
function
(c) 1 point for saying y¢¢ = –2 (or downward), and 1 additional point for
saying that this is true for all x
(d) 1 point for saying “greater than,” and 1 additional point for a valid
explanation
|
|
|
T 2/28/06
|
HW due:
With your study buddy, argue over the accuracy of both answer keys from
yesterday’s assignment. Make sure that you eventually come up with two sets
of correct answers. Additional problems to write out: §8-2 #24, 26, 41.
Bonus Opportunity: Score your re-test from yesterday (from memory), using the
scoring rubric provided above. You will come up with a number from 0 to 18.
If your score matches the score I compute for you, you will earn 2 bonus
points. If you did not take the re-test, then take the entire test (under
time pressure), using a blank copy, and score it.
|
|

