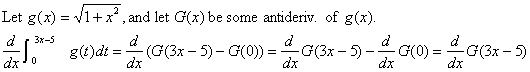Monthly Schedule

(AP Calculus AB, Period A)

M 1/2/06	No school.
T 1/3/06	Classes resume. Here is a practice midterm exam that you can use to keep your brain from decaying over the break. Omit #9(b) and #13(e), which were designed for Honors AP Calculus students. Problems #7 and #8 are at your level, but we have not covered that material yet. (The practice exam is somewhat harder than the one you will be taking, but you should be able to do it. This is a bit like swinging with two bats while on deck. By the time you face the pitcher, you should be able to move a single bat with good speed.) Other study suggestions: (1) a good AP review book, such as the Barron’s or Princeton Review series, and (2) flash cards or other means to make sure that you know 100% of the things that you are supposed to know cold, such as the standard derivative and antiderivative formulas. In class: Group purity quiz. Here are questions 13-17, which we did not have time to cover when time ran out.
W 1/4/06	Purity Quiz #1 (10 pts.) in preparation for midterm exam. There is no partial credit. The question will be similar in spirit to those presented in class yesterday. There is no additional HW due, but please have your notebook and equipment on hand for possible spot checks throughout the week. Please work on the practice midterm exam and read the information about it under yesterday’s calendar entry. I will be delighted to answer questions related to the practice midterm or anything else you may be confused about.
Th 1/5/06	Purity Quiz #2.
F 1/6/06	Purity Quiz #3. HW due (max. 35 minutes, as announced during class): 1. Compute Use the quotient rule. 2. Repeat #1 by using the product rule. (Multiply through by y^2 before differentiating.) 3. Use algebra (good practice) to show that your answers to #1 and #2 are equal. Pacing: 2 minutes for #1, 2 minutes for #2, ? for #3.
M 1/9/06	Midterm Exam, 8:00–10:00 a.m., Room S. The exam counts as 20% of your semester grade. The format will be a mixture of short answer, multiple choice, and free response. If you bring a neatly filled-out copy of the practice midterm exam (omitting questions 7, 8, 9b, and 13e), 2 bonus points will be added to your exam score. Yes, neatness counts. You can earn 1 additional bonus point by bringing a spare set of batteries for your calculator. Calculator and pencils are required equipment and will not be furnished if you forget them. You may also use a pen if you prefer, but your name and any bubble-sheet fill-ins must be written in pencil. In short answer and multiple choice, anything goes (other than looking at your neighbor’s paper, of course). For free response, the four permitted graphing calculator operations are MATH 8, MATH 9, MATH 0, and the sketching of a graph. By “permitted” I mean that you never have to show any work to justify the answers that those four operations produce. However, in problems where work must be shown, you may not use the calculator alone to claim the maximum or minimum of a function, nor to draw a conclusion from the shape of a graph (e.g., “The function is increasing because the graph appears to be sloping upward”). Instead, you must analyze the derivative and draw conclusions based on the sign of the algebraic expressions that result. Technically, you are also not permitted to use your calculator to find derivative functions or antiderivative functions, but in practice there is no way for the AP graders to enforce this rule. (Note: MATH 8 is the derivative at a point, not the derivative as a function.) Because some AP students use calculators (e.g., TI-92) that have symbolic algebra capabilities, the AP exams are constructed in a way to minimize the advantage for students who have such calculators.
M 1/16/06	No school.
T 1/17/06	No school.
W 1/18/06	Classes resume. Homework amnesty for the first semester is now in effect. Most students now have 10 bonus points for the third quarter and fresh cuts for the second semester. Please review my attendance policies, and remember that excused absences that are not reported in a timely fashion are considered cuts. You might also want to review the homework guidelines so that you will earn 4/4 each time your HW is scanned. In class: Easy quiz on alphabet, lower case Greek letters (alpha, beta, gamma, delta, theta, mu, pi, rho, sigma, phi, chi, psi, omega), upper case delta, digits 0-9, the spelling of the word “theorem,” EVT/IVT/MVT/FTC1/FTC2, the course objectives, and Mr. Hansen’s objective.
Th 1/19/06	HW due: Read §6-3; write §6-2 #1-4 all, 11; write §6-3 #3-45 mo3, #47-50 all. (If you get bogged down, you may omit a few without penalty.) The easiest problems are #47-50, which you should be able to in less than 15 seconds each. Seriously.
F 1/20/06	HW due: Write §6-3 #51-54 all, and prepare #1-50 for oral presentation. Here is a worked version of #53 to get you started: (The reason for the last step is that G(0) is a constant.) By def. of G and by the chain rule, we have as given on p. 706.
M 1/23/06	HW due: Write §6-3 #27-54 all. Since these problems were all previously assigned, you may already have them already written out, in which case you have no additional work to do. Here is a worked version of #35 to help you: 35. Let u = 1 + sec x, du = sec x tan x dx. Then
T 1/24/06	HW due: Read §§6-4 and 6-5; write §6-4 #7, 10, §6-5 #1-15 odd, 24. Try to use the technique of logarithmic differentiation (take log, then differentiate both sides of equation, then solve for the derivative). Bonus opportunity: Try solving any of the Mathcross puzzles other than the ones for which solutions have already been circulated. I will award a 5-point bonus for the first completely correct solution received for each puzzle (limit one per student).
W 1/25/06	HW due: Read §6-6, much of which is review; write §6-6 #5-14 all.
Th 1/26/06	HW due: Read §6-7; write §6-6 #19, §6-7 #5-60 mo5, 63.
F 1/27/06	HW due: Read §6-8; write §6-8 #2-24 even. Note: Each time you apply L’Hôpital’s Rule, show the proper abbreviation in parentheses in the margin, either (0/0 L’Hôp.) or (¥/¥ L’Hôp.). That is so the reader can tell when a L’Hôpital transformation has occurred. Otherwise, the reader can become confused, because normally we expect only algebraic transformations to be occurring from one line to the next. Also note: You must write the word “lim” on each line. If you leave out the word “lim,” your equalities are not true statements. Final note for A+ students only: The equalities in L’Hôpital’s Rule problems are “provisional” in the sense that the chain does not hold unless the final limit evaluates to a number and (see MathWorld) the denominator derivative does not change sign infinitely often in a neighborhood of interest. Your book (see p. 285) omits the second proviso, since most high school students cannot understand it. Fortunately, L’Hôpital’s Rule on the AP exam applies only to simple cases, and even then only on the BC exam. If the “latter limit” that your book refers to is DNE (i.e., if the limit of the derivatives’ quotient is DNE), then L’Hôpital’s rule gives no information. Exception: If the latter limit is +¥ or –¥, as opposed to a “true DNE,” then the original limit would be the same as the latter limit.
M 1/30/06	No additional HW due today. However, you should work on tomorrow’s assignment, especially if you are in Form V. (Juniors have College Night tonight and will be squeezed getting the Tuesday HW finished unless they start over the weekend.)
T 1/31/06	“HW and a Half” due: Read §6-9; write §6-8 #25, 26, 28 (approx. 3 minutes each); §6-9 #5-85 mo5 (30 seconds each), 86, 88. You should be able to produce the answers for 1-80 almost instantly if asked in class. The total assignment should take you approximately 55 minutes. If it takes you much longer than that, then you have a clue that you are not yet ready for the test.

---

Return to the Calculus Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 03 Feb 2006