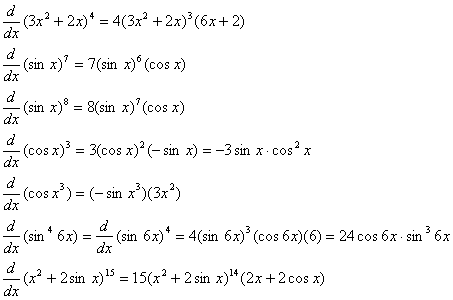|
M 10/3/05
|
HW due:
Patch up your existing HW through §2-6 and add these “additional problems”:
A1. Use a sketch to show that the Intermediate Value Theorem’s hypothesis
that f (x) is continuous on a closed
interval [a, b] is important. In other words, show
why the IVT’s conclusion need not be true if f (x) is continuous
merely on an open interval (a, b).
[Recall that an open interval is an interval such as the set of x values where –2 < x < 3, i.e., an interval that does
not include its endpoints. A closed interval is an interval such as [–2, 3]
that does include its endpoints. Intervals like (–4.1, 7] or [3, 9.2) are
called “half-open or half-closed intervals” depending on one’s mood.]
A2. The conclusion of the IVT (green box on p. 67) would still be true if
worded, “. . . then there is a number x
= c in [a, b] for which f (c)
= y.” Explain why, and then explain
why the theorem was written in the form in which it was written. (This is not
really a mathematical question. It is more of a philosophical question.)
|
|
|
T
10/4/05
|
HW due (as given orally during class 10/3): Find a real-world
application of the result of yesterday’s quiz. In other words, given two
continuous functions f and g, where h(x) = f (x)
– g(x), find an interpretation that makes these functions something
of other than merely abstract interest. You may use the Internet to assist
your search, but I doubt you will find the problem posed (or solved) in
precisely this format. In other words, you will need to understand and adapt
whatever you find in order to fit the conditions posed. Hint: The circumference of the earth is about 50,000 units if you
use a unit of approximately half a mile.
For those who have forgotten the original question, here it is again:
Given: Let f and g be continuous on [0, 25000], and let
f (0) – g(0) = g(25000) – f (25000) ¹ 0.
By #2 on the quiz, we decided that h(x) = f (x) – g(x)
is also continuous on [0, 25000]. Let q
= f (0) – g(0). Then h(0) = q and h(25000) = –q. In other
words, h(x) changes sign on [0, 25000], since q is known to be nonzero. Therefore, by IVT, there must exist at
least one value c Î (0, 25000) such that h(c) = 0. But saying h(c)
= 0 is equivalent to saying f (c) – g(c) = 0, i.e., f (c)
= g(c). Here is that conclusion in English: f and g must intersect
at least once between 0 and 25000.
Your task is to find a concrete application of that conclusion to the real
world. For your answer, state precisely what f and g should be
defined to be, and state precisely the interesting conclusion that IVT allows
you to draw.
|
|
|
W
10/5/05
|
HW due:
Continue working on yesterday’s problem, and add §2-6 #10, 12, 13.
Hints: One effective strategy in
Web searching is to imagine words that would appear in a page that some
mathematician, somewhere, might have written on the subject. For example, it
is a safe bet that at least one of the pages relevant to this discussion
would use the phrase “intermediate value theorem” along with the phrase
“consequence” or even “remarkable consequence.” Now here is where good
students can distinguish themselves from the ordinary. An ordinary student,
noticing that none of the Web pages seem to be leading anywhere (or even seem
to be intelligible by human beings), will simply give up at this point. The
good student will try to find some unusual word or phrase in a promising Web
page and will use that as a lever to try to crack the problem open, searching
for that term in addition to (or instead of) some of the keywords previously used.
You can also make use of some of the ideas students mentioned in class:
world, equator, longitude, circumference. Those may or may not be helpful,
but they certainly give you many avenues to explore and will generate many
additional possible keywords.
|
|
|
Th 10/6/05
|
HW due:
Read §3-2; write §3-2 #15.
|
|
|
F 10/7/05
|
No school.
|
|
|
M 10/10/05
|
No school.
|
|
|
T 10/11/05
|
HW due:
Read §3-4 (reading notes required); write §3-3 #1, 7, 11. Reading notes for
§3-3 are not required.
|
|
|
W 10/12/05
|
Test on Chapter 2 only. You need to know your IVT and EVT cold, plus
“extended reasoning and explanation” questions of the type we did in class
yesterday. Other sample questions can be found in the practice test on pp.
74-76.
|
|
|
Th 10/13/05
|
No additional HW due.
Please enjoy a well-deserved day of rest. If you are behind on your homework
(or if, for example, you forgot to use the “limit of difference quotient”
method of §3-2 when answering §3-3 #11ac), you can use this time to patch up
the loose ends.
|
|
|
F 10/14/05
|
HW due:
Read §3-4 or write §3-4 #2-18 even.
If you feel comfortable doing both, that is also fine. If you choose the
reading assignment, remember that reading notes are required, as always.
Let me explain what is meant by good reading notes. Usually, merely copying
the contents of the green boxes is not particularly helpful. (It is certainly
easy, but if you are spending the time to do it, why not choose something
that is educationally worthwhile for you?) Better ideas including the
following: (1) paraphrasing the
green boxes in your own words, (2) writing specific questions to pose in
class the next day, or (3) working example problems that are suggested to you
by the textbook reading.
|
|
|
M 10/17/05
|
HW due:
Write §3-4 #23-26 all, plus do the other half of Friday’s assignment. (If you
already did both the reading notes and the problems for Friday, so much the
better.)
|
|
|
T 10/18/05
|
Form VI retreat (no class).
|
|
|
W 10/19/05
|
HW due:
Write §3-4 #39, §3-5 #1, 2, 6, 7, 8.
|
|
|
Th 10/20/05
|
HW due:
Write §3-5 #3, 4, and find a parametric representation that produces the
ellipse
x2/4 + y2/9 = 1. (Also graph it on
your calculator using a suitable window.)
|
|
|
F 10/21/05
|
HW due:
1. For the iterated function f (x) = ax(1 – x), make a table
and a fairly good sketch of the long-term behavior (i.e., limit(s) as f (f
(f (f . . . (x)))) is
iterated arbitrarily many times) versus a.
In other words, you will have a table like the one we made, only more
complete, and a graph resembling the one we made in class yesterday. Let a go from 2 to 5 in increments of 0.2.
Your horizontal axis will be the a
axis, and the vertical axis will indicate the long-term point(s) of
stability.
2. Does your graph of long-term point(s) of stability versus a represent a function? Why or why
not?
3. Use the forward, backward, and symmetric difference methods to estimate
the derivative (with respect to a)
of the graph you found in #1 at the point a
= 2.6.
4. What is the second derivative when a
= 2.6? How do you know?
Hints for students who missed class
Thursday or who were not paying attention: Start with x = 0.6 each time. (On calculator: 0.6
STO X ENTER.) Then let a be the
parameter value of interest. (For example, 2.6 STO A ENTER, where A is
entered using the ALPHA key.) Then press ENTER a few dozen times, or write a
program to accomplish this, until the long-term behavior of the iterated
function starts to be clear.
|
|
|
M 10/24/05
|
HW due: Read
§§3-6 and 3-7. See if you can “imagine” how to explain the mechanical
workings of the chain rule by reading the examples below. After you think you
understand what is going on, quiz yourself by covering up the answers and
seeing if you can reproduce the answers on your own.
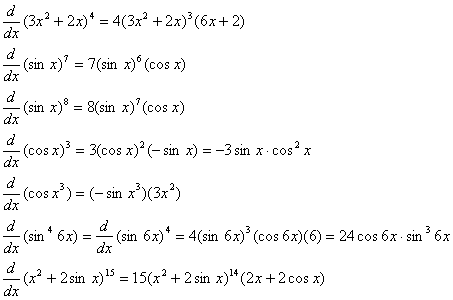
Then write §3-7 #1-22 all. Also, if your answers to Friday’s questions 2, 3,
and 4 differ significantly from those below, then rework Friday’s assignment.
2. No, since from the first point of bifurcation onward, there is no longer a
unique y corresponding to each x in the domain.
3. Using h = .00001, we get
.147928516 as a forward difference estimate, .147929579 as a backward
difference estimate, and .1479290475 as a symmetric difference estimate.
4. By estimating the derivative at 2.60001 to be .147927349 (forward
difference method), and comparing that with .147928516 from #3, we can use a
forward difference method on the derivative
values to get a forward difference estimate of the second derivative, namely
–.1167. The sign is reasonable, since from our sketch we can see what appears
to be downward concavity (i.e., decreasing first derivative).
|
|
|
T 10/25/05
|
HW due:
§3-8 #1, 4, 13; §3-9 #2-24 even. Note:
This sounds like a lot of problems, but the ones in §3-9 are very short, and
#2-16 can all be done in about 20 seconds each. (I timed myself.) True,
#18-24 take somewhat longer, but you need to build up speed and proficiency
with those as well. I would like you to write out your problems in the manner
shown below. If you get stuck, you may adapt the solution from the
corresponding odd-numbered problem that precedes your problem. For example,
#1 shows how to do #2, #3 shows how to do #4, and so on. Try to work without
peeking too often, since you will learn more that way.
Also note: Simplification is not
required. Explanations in [square brackets] are not expected to be written
out as part of your solutions.
1. f ¢(x) = 7x6 Þ f (x) = ò 7x6
dx = x7 + C
3. f ¢(x) = x5 Þ f (x) = ò x5
dx = x6/6 + C
5. f ¢(x) = x–9 Þ f (x) = ò x–9
dx = x–8/(–8) + C
7. f ¢(x) = cos x Þ f (x) = ò cos x dx = sin x + C
9. f ¢(x) = 36x7/2 Þ f (x) = ò 36x7/2
dx = 36x9/2/(9/2) + C
= 8x9/2 + C [simplification optional]
11. f ¢(x) = sin
5x Þ f (x) = ò sin 5x dx = (–cos 5x)/5 + C
13. f ¢(x) = (4x + 5)7 Þ f (x) = ò (4x + 5)7
dx = (4x + 5)8/8 · ¼ + C
[Do you see how multiplying by ¼ accounts
for the chain rule, in reverse?]
15. f ¢(x) = x2 + 6x – 5 Þ f (x) = ò (x2 + 6x – 5) dx = x3/3 +
6x2/2 – 5x + C
17. f ¢(x) = x4 Þ f (x) = ò x4
dx = x5/5 + C
f
(1) = 10 [given]
15/5 + C = 10 [by subst.]
C
= 10 – 1/5
C
= 9.8
f
(x) = x5/5 + 9.8
19. f ¢(x) = cos x Þ f (x) = ò cos x dx = sin x + C
f
(p/2) = 5 [given]
sin(p/2) + C =
5 [by subst.]
1 + C
= 5
C
= 4
f
(x) = sin x + 4
21. f ¢(x) = x2 – 8x + 3 Þ f (x) = ò (x2 – 8x + 3) dx = x3/3 –
8x2/2 + 3x + C = x3/3 – 4x2 + 3x + C
f
(–2) = 13 [given]
(–2)3/3 – 4(–2)2 +
3(–2)+ C = 13 [by subst.]
–8/3 – 16 – 6 + C = 13
C
= 113/3
f
(x) = x3/3 – 4x2
+ 3x + 113/3
23(a). d ¢(t) = 70 –
9.8t Þ d (t) = ò (70 – 9.8t)
dt = 70t – 9.8t2/2
+ C
Answer [simplification
optional]: d(t) = 70t – 4.9t2 + C
(b). d(0) = 6
[given]
70(0) – 4.9(02) + C = 6
0 + C = 6
C = 6
d(t) = 70t – 4.9t2 + 6
(c). d(5) = 70(5)
– 4.9(52) + 6 = 233.5 m
d(6) = 70(6) – 4.9(62) + 6 = 249.6 m
d(9) = 70(9) – 4.9(92) + 6 = 239.1 m
By EVT, d(t) has a maximum
value ³ 249.6 m somewhere between
t = 5 and t = 9.
(d). Quadratic fcn. d(t) is differentiable on [5, 9]. Since
the max. value cannot occur
at an endpt., max. must occur
when d ¢(t) = 0.
Therefore, set d ¢(t) = 0
and solve for t. [Note: The preceding explanation is required.]
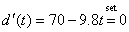
9.8t = 70
t » 7.143 sec [Note:
The book’s answer is inadequate. AP standard is 3 decimal places.]
d(t) = 256 m at
that time [by calc.]
|
|
|
W 10/26/05
|
No additional HW due.
In class: Review.
|
|
|
Th 10/27/05
|
Test on Chapter 3.
The format is multiple choice, no partial credit, no calculator. A few
questions may require knowledge of IVT and EVT. See, for example, the
explanation for #23c in the 10/25 calendar entry.
There will be 16 questions, with a time limit of 32 minutes for regular time
or 48 minutes for extended time. In accordance with AP scoring guidelines,
there is a point penalty for each incorrect answer. Point values are 0 for an
omission, 4 for a correct response, –1 for an incorrect response. Your name
is worth 36 points. There will be no additional curve.
Be sure to practice your speed and proficiency, since you have only 2
minutes per problem on average (3 minutes for extended-time students).
Here are some practice questions to help you become familiar with the format.
A few of them are intended for honors students only, and #9 in the second set
covers material we have not seen yet. However, the rest of them are good
practice, and they certainly illustrate the format so that you can get some
practice. See an AP review book (Barron’s, Princeton Review, etc.) if you
desire more practice problems.
-- Multiple choice practice #1
with answer key
-- Multiple choice practice #2 with
answer key
|
|
|
F 10/28/05
|
No additional HW due today.
Some old HW may be checked.
|
|
|
M 10/31/05
|
HW due:
§4-2 #4-20 mo4, 20, 23; §4-3 #4-24 mo4, plus repeat #4 from §4-2 using QR
instead of PR. Reading notes are optional.
|
|