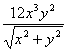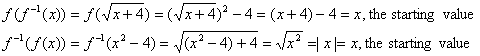|
1.
|
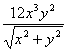 (instant DQ for
trying to simplify the denominator)
|
|
|
|
|
|
|
|
2.(a)
|
1.5 [Hint: Think of 24 as 3 · 4 · 40.5.]
|
|
(b)
|
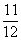 [Hint: Think of 4Ö3 as 4 · 30.5.]
|
|
|
|
|
3.(a)
|
a set of ordered pairs
|
|
(b)
|
a relation in which each x in the domain has a unique y in the range
Also acceptable: a relation in
which y is uniquely determined by x
|
|
(c)
|
a function in which each y in the range has a unique x in the domain
Also acceptable: a function in
which x is uniquely determined by y
Not acceptable: a relation in which
x is uniquely determined by y
Explanation for why third version is not acceptable: A vertical line (e.g., x = 3.2) shows that a relation can
easily have the property of having x
uniquely determined by y. However,
nobody would claim that the vertical line x
= 3.2 describes a one-to-one function.
|
|
|
|
|
4.
|
C
|
|
|
|
|
5.
|
B (one-to-one)
|
|
|
|
|
6.
|
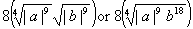
Explanation: Since the original expression is valid for any values of a and b, regardless of sign, we have to make
sure that the simplified expression returns the same results. The absolute
value bars accomplish this goal. If you missed this fine point, but if
everything else in your answer is correct, score 9.5 out of 10. In Precalculus, the point penalty would be more significant.
Here is a simpler example to illustrate the point:
What is (x6)0.5?
You might be tempted to say 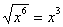 , but that would be invalid if x is a negative number (say, –2). After all, the square root of
(–2)6 is the square root of 64, which is simply 8, and 8 ¹ (–2)3. The correct simplification of (x6)0.5 is |x|3.
|
|
|
|
|
7.(a)
|
Inverse relation is {(3,
1), (4, 2), (8, 3), (7, 4)}.
Your plot should consist of only those four points—not connected. That’s right, the relation is four disconnected
points, and so is its inverse.
|
|
(b)
|
Fcn. y = 2 log4 3 ≈ 1.6, a horizontal line
Inv. x = 2 log4 3
≈ 1.6, a vertical line (plot line on a rough sketch
showing tick marks at 1 and 2)
[Note that the inverse is not a function.]
|
|
|
|
|
8.
|
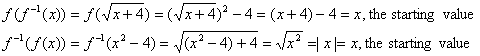
For full credit on corrections, work vertically (one = sign per line), and provide
a brief reason for each step. For example, the final step in the second proof
is justified because |x| = x when x ³ 0. During the test itself, steps were required but a justification
of each one was not expected since time was so short.
|