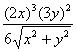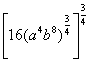Algebra II / Mr. Hansen
12/1/2005

Name: _________________________
(6 pts.)

Test on Chapter 6, Excluding §§6-13 and 6-14

Time limit: 24 minutes (36 minutes for extended time). Calculator is allowed throughout.
Point values are shown in parentheses. Your name is worth 6 points.

 

1.

(8 pts.)

Simplify:

 

 

 

 

 

 

2.

If log8 3 ≈ .5 and log8 4 ≈ ⅔, estimate

(a)
(8)

log8 24

 

 

 

 

 

 

(b)
(8)

log8 4Ö3

 

 

 

 

 

 

3.

Define each of the following:

(a)
(6)

relation

 

 

(b)
(6)

function

 

 

(c)
(6)

1-to-1 function

 

 

4.

(5)

Which relations have an inverse relation? (Mark one.)
A) None
B) Some (only the ___________________ ones) (fill in if used)
C) All

 

 

5.

(5)

Which functions have an inverse function? (Mark one.)
A) None
B) Some (only the ___________________ ones) (fill in if used)
C) All

 

 

6.

(10)

Simplify:



Convert so that your final answer uses only integers as exponents.

 

 

 

 

 

 

 

 

7.

State and sketch the inverse of each relation.

(a)
(10)

Consider the relation defined by {(1, 3), (2, 4), (3, 8), (4, 7)}.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(b)
(10)

f (x) = 2 log4 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.

(12)

Let f (x) = x2 – 4, x ³ 0. Prove that f –1(x) =  by evaluating f (f –1(x)) and f –1(f (x)). Show all details (i.e., the steps in the evaluation of those two expressions).

[Note: During the test, many students misunderstood this problem, apparently thinking that they had to derive the inverse. However, the inverse has already been provided. The only thing left to do is to prove that the function f and its claimed inverse fit together properly. This problem is similar to HW problems due on 11/22/2005. In fact, you should read the 11/22 comments in the archives. In problems #21-26 in §6-12, you were given two functions, f and g, and by looking at f (g(x)) (and for thoroughness, g(f (x)), though the book did not ask for that), you can determine whether f and g go together as a function-inverse pair. Here is the key idea: Does running x first through one “kerchunka” machine and then the other take you back to where you began?]

[Technical note: The requirement that x ³ 0 for the domain of f was inadvertently omitted on the original version of the test. Having x ³ 0 guarantees that f is one-to-one, hence invertible. Students who noticed that earned a bonus point. Since f is invertible, f –1 is guaranteed to exist. All you have to do is to prove that the claimed f –1 function really works as it should.]