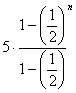Algebra II / Mr. Hansen 4/7/2006

Name: ______E period KEY______ (10 pts.)

Test on Chapter 11: Sequences, Series, Binomial Theorem

Time limit: 26 minutes. A calculator is required.
Each problem is worth 3 points. There is no partial credit. Write the capital letter of the
best choice, or fill in the word or phrase that best fits each blank.

	Class statistics: n = 9 s = 16.9 (standard deviation) median = 74.5 low score = 37 high score = 91
1.	B
2.	C
3.	D
4.	E
5.	A
6.	A
7.	C
8.	d [must be lower case for credit]
9.	|r| < 1
10.	4/3 by the infinite sum formula
11.	DNE
12.	B
13.	D
14.	plug-ins [or substitutions]
15.	units
16.	tn = t1 + (n – 1)d
17.	t741 = 55 + 740(–11)    [Note: The –11 must be enclosed within parentheses to earn full credit.]
18.	= –8085
19.	[Note: This is the only valid formula that qualifies for points.]
20.	Since we want , plug in values to get > 9.9995.
21.	Use guess-and-check to find n, or solve the inequality above for n to get answer: n ³ 15. Here are the details:
22.	C
23.	C
24.	E [coefficient should be 84, not 122]
25.	D
26.	B
27.	3 + 5 + 7 + . . .
28.	Sn = n(t1 + tn)/2
29.	S200 = 200(3 + 401)/2 = 200(404)/2 = 100(404)
30.	= 40,400 Note: While it is true that the instruction “. . . and then compute the sum” could conceivably be interpreted to mean 3 + 5 + 7 = 15, this interpretation is inconsistent with the later instruction to “show all three components of your proper work.” Surely it is not reasonable that 9 points (problems 28, 29, and 30) would be set aside for adding 3 + 5 + 7 after you had already listed them in problem #27. Therefore, students who merely added 3 + 5 + 7 earned half of the 12 total points available in this section. On Monday’s test, I will make the instructions clearer if there is a question of this type.