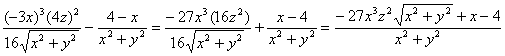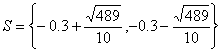Algebra II / Mr. Hansen 1/23/2006

Name: _________________________ (2 pts.)

Answer Key for Test on Chapter 7

1.
(a) (8 pts.)
	Note: You must cross your “z” for full credit.
(b) (4 pts.)	–2.832®[ALPHA] X [ENTER] 7.113®[ALPHA] Y [ENTER] 2®[ALPHA] Z [ENTER]
(c) (4 pts.)	First term = 320.404896 . . . Second term = 0.116557 . . . Difference = final answer = 320.288
(d) (4 pts.)	Numerator = 18773.69874 . . . Denominator = 58.614993 Quotient = final answer = 320.288
(e) (5 pts.)	NO, since either (1) the values could have been “lucky” values that simply allowed the answers to turn out equal, or (2) the answer might not have been fully simplified. However, the truth is that finding (c) equal to (d) is strong evidence suggesting that you did the work correctly.
2.	Note: The equation has solutions precisely where f (x) has roots. Therefore, students who found roots of f (x) using their calculator were actually answering the same question as the question about solving the fractional equation.
(a) (4 pts.)	Df = Â \ {–2, 3}
(b) (12 pts.)	Multiply both sides by (x + 2)(x – 3). After several lines of algebra, you should obtain the quadratic equation –5x^2 – 3x + 24 = 0, which can be solved by the quadratic formula.
(c) (6 pts.)	S = {–2.511 . . . , 1.911 . . .}
(d) (5 pts.)	Method 1 (boring): Use calculator to evaluate the quadratic formula expressions. Method 2 (better, since it provides a cross-check): Use 2nd CALC zero to find the zeros of function f. Method 3 (creative, fun): Set Y2=X/(X+2)–4 and Y3=2X/(X–3). Use 2nd CALC intersect to find the places where the two functions (i.e., LHS and RHS of original fractional equation) are equal to each other. Method 4 (fun, but time-consuming): Enter function f into Y1 and use 2nd TBLSET to set the independent variable to “Ask” mode. Then press 2nd TABLE and stab around at various values for X until you find the ones that make Y1 as close to 0 as possible.
(e) (8 pts.)	To perform a proper “check,” you must go all the way back to the original fractional equation. Plugging in –2.511 . . . gives 0.9113344 . . . on both the LHS and the RHS. Plugging in 1.911 . . . gives –3.5113344 . . . on both the LHS and the RHS. It looks as if both values do indeed satisfy the original fractional equation.
(f) (6 pts.)	Both solutions check, and neither solution clashes with –2 or 3, which were excluded because of the need to avoid division by 0.
(g) (6 pts.)	Punch f into Y1 if you have not already done so, and press ZOOM 6. Use dotted lines for the vertical asymptotes at x = –2 and x = 3. Use arrows to indicate that the curve continues infinitely downward, upward, and to the left and right. It is good to show the y-intercept at (0, –4), as well as the horizontal asymptotes at y = –5. However, I did not deduct points for these omissions, because I had not been clear about what level of detail would be required.
3.
(a) (2 pts.)	50.07%; yes
(b) (2 pts.)	2.77 (reading comprehension check)
(c) (5 pts.)	Let x = sample size (# of likely voters polled). Let y = m.o.e. (in % points). Note that y depends on x.
(d) (4 pts.)
(e) (8 pts.)	The sketch should show an L-shaped curve in the first quadrant. By using the fact that y = 2.77 when x = 1250, you can solve for k. You should have obtained k = 2.77(1250)^0.5 » 97.934289. p.e.:
(f) (5 pts.)	Plug into the p.e.:
(g) (5 pts.)	Use the p.e. again, but this time set y = 1.5 (E period) or y = 1.3 (F period) and solve for x. The fastest way is probably to plot the p.e. as a function and see where it intersects the appropriate horizontal y line. However, you can also use old-fashioned algebra. Answer (E period): 4263 people Answer (F period): 5676 people (Note: You must round up in both cases, despite what you might think the rules of rounding would suggest. This is similar to the old IQ question about how many school buses are needed to transport 55 students if a bus holds 50 students. The answer is not 1.1, obviously, but it cannot be rounded to 1, either. The correct answer is 2.)