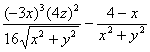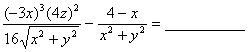Algebra II / Mr. Hansen 1/23/2006

Name: _________________________ (2 pts.)

Test on Chapter 7

Time limit: 36 minutes (48 minutes for extended time). A calculator is required.
Point values are shown in parentheses. Your name is worth 2 points.

1.
(a) (8 pts.)	Subtract fractions and simplify the result:
(b) (4 pts.)	Use your calculator to “STO” the meaningless value –2.832 into x and the meaningless value 7.113 into y. Raise your hand either to show me that you have accomplished this task, or to ask me to do it for you (in which case I will charge you the 4 points).
	Mr. Hansen’s initials to certify completion: ___________
(c) (4 pts.)	Use your calculator to compute the original expression above, using the meaningless values of x and y from part (b). Let z = 2. Give answer correct to 3 decimal places.
(d) (4 pts.)	Use the meaningless values from part (b), and treat z as being 2, to compute the value of your simplified answer to part (a). You can earn full credit for this portion even if your answer to part (a) is incorrect. Give answer correct to 3 decimal places.
	Answer: _____________
(e) (5 pts.)	If part (c) and part (d) were equal, would that prove that you had carried out the simplification correctly in part (a)? Circle one: YES   NO Why or why not? ____________________________________________________
2.	Consider this fractional equation:
(a) (4 pts.)	State the domain of f if . Df = _____________
(b) (12 pts.)	Give the solution set of the fractional equation in exact (radical) form. Show your work.
	S = ________________________________________
(c) (6 pts.)	Use your calculator to find the solution set as decimal value(s) correct to at least 3 decimal places.
	S = ________________________________________
(d) (5 pts.)	Briefly describe the calculator method you used. (There are many different ways that are possible.)
	________________________________________________________________
	________________________________________________________________
	________________________________________________________________
(e) (8 pts.)	Check your solution. You can earn full credit for this portion, even if your solution above was wrong, by demonstrating that your solution is wrong. However, if your solution is correct, you must demonstrate here that it is correct.

(f) (6 pts.)	Explain why there are no extraneous solutions.
	________________________________________________________________
	________________________________________________________________
(g) (6 pts.)	Sketch the function f that was defined in part (a). If there are any vertical asymptotes, show them as vertical lines.
3.	Whenever two candidates have roughly equivalent popularity, the margin of error (m.o.e.) of a political poll is inversely proportional to the square root of the sample size. For example, suppose that in the election of 2000, St. Albans alumnus Albert Gore, Jr., was favored by 48.1% of those surveyed in one poll, while George W. Bush was favored by 47.3%. If the sample size was 1250 people, the margin of error would be 2.77%.
(a) (2 pts.)	To put it another way, that means that Bush’s support could easily be anywhere between 44.53% and _______________, because of the margin of error. Do you see why the election was so difficult to predict?
(b) (2 pts.)	OK, let’s summarize what we know. M.o.e. varies inversely with the square root of the sample size. With a sample size of 1250, m.o.e. equals __________ percentage points.
(c) (5 pts.)	Define your variables in this problem and indicate what depends on what.
(d) (4 pts.)	Write a general equation. Raise your hand when you reach this point, because if you get this wrong, you won’t be able to continue.

(e) (8 pts.)	Make a sketch and develop a particular equation.
(f) (5 pts.)	Show that the m.o.e. for a sample size of 1400 is about 2.62 percentage points.
(g) (5 pts.)	Compute the required sample size to make the m.o.e. shrink to 1.3 percentage points. Surprised?
BONUS (1 pt.)	Design a logo for the particular equation.