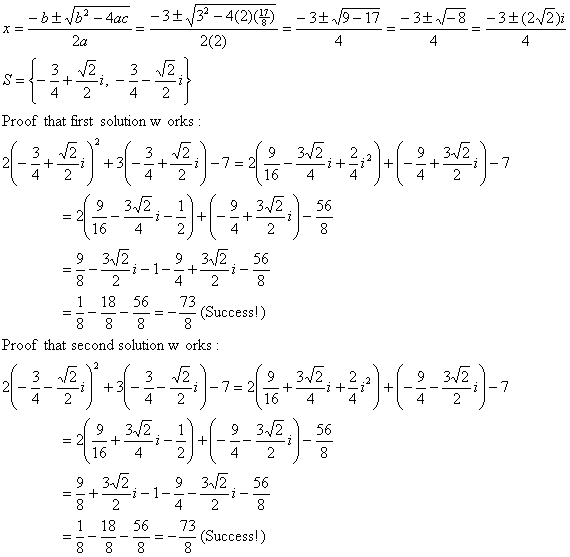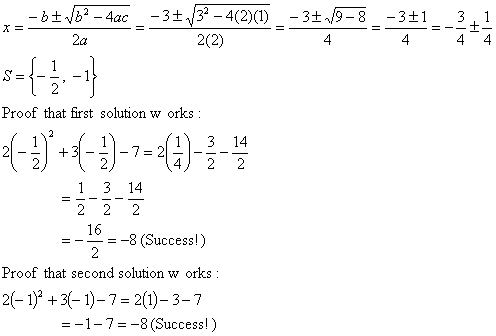Algebra II / Mr. Hansen 10/23/2005

Name: _________________________

Answers to Additional Review Problems Through §5-5
(Supplement to Cumulative Review, pp. 224-227)

	WARNING: Please do not look at these answers until after you have answered all, or nearly all, of the questions.
11.	relation, x, y, well-defined
12.	quadratic, 2
13.	–7, y
14.	–2, no, since f (1) ¹ 0
15.	2, since b^2 – 4ac = 3^2 – 4(2)(–10) > 0
16.	2, since b^2 – 4ac = 3^2 – 4(2)(–7) > 0
17.	1, since b^2 – 4ac = 3^2 – 4(2)(1.125) = 9 – 8(9/8) = 9 – 9 = 0 Since the discriminant is 0 [as shown in prev. line], the solution is x = (–b ± 0)/(2a) = –3/4. S = {–3/4}.
18.	x = –3/4 is the equation, since the axis of symmetry passes through the vertex of the parabola, and the vertex always occurs at the place where the function touches a single y value (as in #17). To see this more clearly, plot the function y = 2x^2 + 3x – 7 on your graphing calculator and note that the vertex occurs at the point (–3/4, –65/8).
19.	none, since b^2 – 4ac = 3^2 – 4(2)(3) < 0
20.	a zero of the function
21.

22.

23.