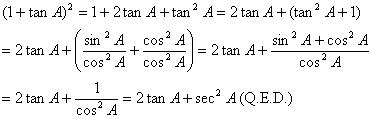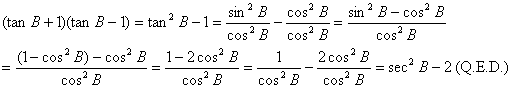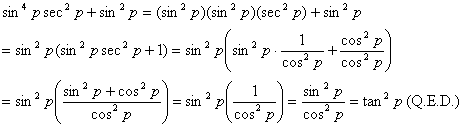Algebra II / Mr. Hansen 5/10/2006

Name: _________________________

Answers to Review Problems Due 5/10/2006

p. 798	T1a. (Ö3)/2   b. –(Ö3)/3   c. p/3     d. 5p/6 (Note: I would also accept –p/6, but 5p/6 is technically more correct, based on the ranges given on p. 771. Of those 6 diagrams, you need to know only the first 3, namely arcsin, arccos, and arctan.)     e. –(Ö74)/7   f. 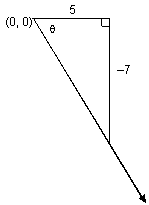540/p Explanation for T1e:     If the ray from the origin passes through (5, –7), then we can sketch a right triangle as follows:     The hypotenuse is Ö74 by Pythag. Thm. By SOHCAHTOA, sin q = –7/Ö74. Therefore, csc q =     reciprocal, as stated above. T2a. cos 37° » 0.6018 by calc.          If you are not allowed to use a calculator, you should be able to estimate as follows:          Since sin 30° = .5, and sin 45° = Ö(2)/2 » .7, sin 37° must be somewhere in between.          A good guess would be 0.6. b. 1/tan(1.9) » –0.3416          Estimating technique: tan 1.9 » tan 2 » tan (2p/3) = –Ö3 » –1.7. Choose a steeper          slope since 2 radians is closer to the y-axis than 2p/3, say –2.5 instead of –1.7. Then          take reciprocal of –2.5, i.e., reciprocal of –5/2, to get –2/5 = –0.4. That is not a great          estimate, but it is acceptable.     c. arccsc 4.5 = “angle whose cosecant is 45/10” = “angle whose sine is 10/45” » 12°50' by calc.          Estimating technique: “angle whose sine is 10/45” » “angle whose sine is 1/4” < 30° since          sin 30° = 1/2. A good guess would be 15° or 20°. d. sin^–1 3 = DNE. You should be able to realize this instantly without a calculator. T3b. amplitude 5, frequency 10 (i.e., 10 cycles in every 360°), centerline y = –3, phase shift = 4° to right
p. 859	R1a.     b. R2a.     b.
p. 879	3. r^2 = 3^2 + 2^2 – 2(3)(2)cos 138° = 21.9177 . . . Þ r » 4.682
	9. 12^2 = 7^2 + 6^2 – 2(7)(6)cos ÐT     144 = 49 + 36 – 84 cos ÐT     144 – 85 = –84 cos ÐT     59 = –84 cos ÐT     –0.70238 . . . = cos ÐT ÐT = arccos(–0.70238 . . .) » 134°37'
	11. 5^2 = 7^2 + 13^2 – 2(7)(13)cos ÐY     25 = 49 + 169 – 182 cos ÐY     25 – 218 = –182 cos ÐY     –193 = –182 cos ÐY     1.0604 . . . = cos ÐY (IMPOSSIBLE!)     No angle has a cosine greater than 1 or less than –1. The triangle (as suggested by the diagram)     is impossible. Answer: DNE.
#18 from 5/8	(a) d^2 = (CN)^2 + (CP)^2 – 2(CN)(CP)cos ÐPCN           = 6400^2 + 6400^2 – 2(6400)(6400)cos (complement of 38°55'44.3")           = 81,920,000 – 82,920,000 cos 51°04'15.7" = 30,445,035.17 . . . d » 5517.703 km
	(b) 6400^2 = 6400^2 + d^2 – 2(6400)(d)cos q, where d was already computed in part (a)     –d^2 = –12,800d cos q d/12,800 = cos q cos q » 0.43107, using previously stored value for d q » arccos 0.43107 . . . » 64°28'
	(c) We know r/d = sin q by SOHCAHTOA.     Since d and q were both found previously, r = d sin q » 5517.703 . . .(sin 64° . . .) » 4978.723 km.
Proba- bility.	P(Mr. Hansen makes at least one shot out of 9) = 1 – P(Mr. Hansen misses all 9 shots)     = 1 – .78^9 = 1 – 0.1068689 . . . » 0.893
	The second probability/counting problem (number of arrangements of king-ace full houses) requires a 4-step analysis: 1. Decide on kings over aces, or aces over kings. (These are different types of hands.) 2. Choose 3 of the more numerous card values. 3. Choose 2 of the less numerous card values. 4. Arrange the 5 cards chosen in steps 2 and 3. Step #1 can be done 2 ways. For each of those, step 2 can be done 4C3 = 4 ways. For each of those, step 3 can be done 4C2 = 6 ways. For each of those, step 4 can be done 5P5 = 5! = 120 ways. Final answer: 2 · 4 · 6 · 120 = 5760.