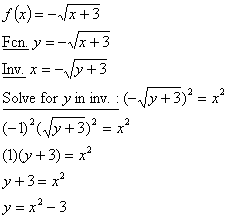|
§6-12
|
|
|
12.(a)
|
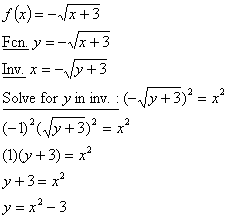
Answer: f 1(x) = x2 3, where x
is restricted to the interval ( ₯, 0].
|
|
|
|
|
Note
|
Why the strange restriction
on x? This, after all, amounts to throwing
away half of a perfectly good parabola. The reason is that f has domain [3, ₯) and range ( ₯, 0], which you can tell by looking carefully at
either the graph of f or the
algebraic definition of f.
Therefore, since f 1
simply flips the roles of x and y, f
1 must have range [3, ₯) and domain ( ₯, 0]. That explains the unusual domain for f 1 given in the answer
above.
|
|
(b)
|
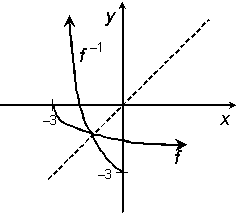
|
|
(c)
|
Yes, f 1 is a function. However, read the note above that explains
why it is not acceptable to define function f 1 merely by writing f 1(x) = x2 3. You must also
restrict the domain of f 1,
i.e., the x values to which f 1 can be applied.
|
|
(more)
|
Note: You
may also be asked to prove that f 1
works as an inverse.
There are two parts to proving this. First, you must show that for any
legitimate value of x, f 1 undoes the action of f, thus taking you back to x. Second, you must show that for any
legitimate value of x, f undoes the action of f 1, thus taking you back
to x.
Part I:
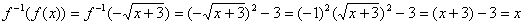
(Q.E.D.)
Part II:
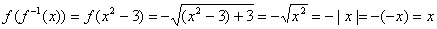
(Q.E.D.)
Part II has some aspects that could be featured on a test. Do you see how the
square root of x2 makes
an appearance? Also note that since x
£ 0 in Part II (because
of the domain restriction for f 1),
the absolute value of x is actually
x, which should be read the
opposite of x since x is certainly not a negative
expression here.
|
|
|
|
|
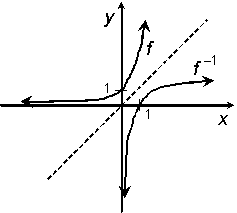
13.(a)
|
f (x) = 1.4x
Fcn. y = 1.4x
Inv. x = 1.4y
Solve for y in inv.: y = log1.4 x [by def. of log]
Answer: f 1(x) = log1.4 x
|
|
(b)
|
|
|
(c)
|
Yes, f 1 is a function.
|
|
(more)
|
As above, let us prove that
the purported inverse works correctly.
Part I: f 1(f (x)) = f 1(1.4x) by subst.
and def. of f
=
log1.4 (1.4x)
by def. of f 1
=
x by def. of log
(Q.E.D.)
Part II: f (f
1(x)) = f (log1.4 x) by subst.
and def. of f 1
=
1.4 raised to the log1.4 x
power by def. of f
=
1.4 to the exponent which produces x
when applied to 1.4 power by def. of log
=
x by def. of log
(Q.E.D.)
|
|
|
|
|
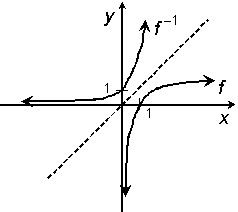
14.(a)
|
f (x) = log2 x
Fcn. y = log2 x
Inv. x = log2 y
Solve for y in inv.: 2x = y [by def. of log]
Answer: f 1(x) = 2x
|
|
(b)
|
|
|
(c)
|
Yes, f 1 is a function.
|
|
(more)
|
As in #12 and #13 above,
you may be asked to prove that f 1
works as an inverse.
I will omit the justifications. Hang on tight! Reread #12 and #13 if any of
this is confusing.
Part I: f 1(f (x)) = f 1(log2 x) by subst.
and def. of f
=
2 raised to the log2 x
power by def. of f 1
=
x by def. of log
(Q.E.D.)
Part II: f (f
1(x)) = f (2x) by subst. and def. of f 1
=
log2 (2x) by
def. of f
=
x by def. of log
(Q.E.D.)
|
|
|
|
|
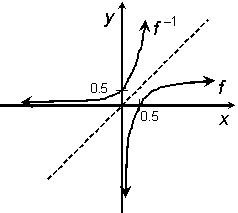
15.(a)
|
f (x) = log5 2x
Fcn. y = log5 2x
Inv. x = log5 2y
Solve for y in inv.: 5x = 2y [by def. of log] ή y = 5x/2
Answer: f 1(x) = 5x/2
|
|
(b)
|
|
|
(c)
|
Yes, f 1 is a function.
|
|
(more)
|
Part I:
f 1(f (x))
= f 1(log5 2x) by subst.
and def. of f
=
half of (5 raised to the log5 2x power) by def. of f 1
=
½(2x) by def. of log
=
x by alg.
(Q.E.D.)
Part II: f (f
1(x)) = f (5x/2) by subst. and def. of f 1
=
log5 (2(5x/2))
by def. of f
=
log5 (5x) by alg.
=
x by def. of log
(Q.E.D.)
|
|
|
|
|
16.(a)
|
g(x) = 60.5x
Fcn. y = 60.5x
Inv. x = 60.5y
Solve for y in inv.: 0.5y = log6 x [by def. of log] ή y = 2 log6
x
Answer: g1(x) = 2 log6 x
|
|
(b)
|
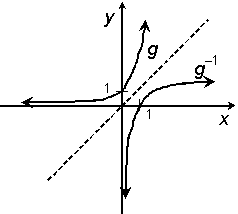
|
|
(c)
|
Yes, g1 is a function.
|
|
(more)
|
Part I:
g1(g(x)) = g1(60.5x) by subst.
and def. of g
=
2 log6 (60.5x)
by def. of g1
=
2(0.5x) by def. of log
=
x by alg.
(Q.E.D.)
Part II: g(g1(x)) = g(2 log6 x)
by subst. and def. of g1
=
6 raised to the ½ (2 log6 x)
power by def. of g
=
6 to the (log6 x) power
by alg.
=
x by def. of log
(Q.E.D.)
|
|
|
|
|
p. 319
|
|
|
R9.(a)
|
log27 j = 2/3
Rewrite as 272/3 = j.
Now, 272/3 = (271/3)2 = 32 = 9.
Answer: j = 9.
[The reason for the substitution is that 271/3 means the cube root
of 27, namely 3.]
|
|
(b)
|
log3 81 = m
Rewrite as log3 34 = 4 log3 3 = 4(1) = 4.
Answer: m = 4.
|
|
(c)
|
logp 343 = 3
Rewrite as p3 = 343.
Take cube root of both sides to get p
= 7.
[The significance of 343, which is 73, is very sad: the number of
NYC firefighters killed on 9/11.]
|
|
|
|
|
R12.(a)
|
f (x) = 7x + 42
Fcn. y = 7x + 42
Inv. x = 7y + 42
Solve for y in inv.: 7y = x 42 ή y = x/7 6
Answer: f 1(x) = x/7 6
|
|
(b)
|
g(x) = log5 3x
Fcn. y = log5 3x
Inv. x = log5 3y
Solve for y in inv.: 5x = 3y ή y = 5x/3
Answer: g1(x) = 5x/3
|
|
(c)
|
h(x) = x2
Fcn. y = x2,
where x ³ 0 (given)
Inv. x = y2, where y ³ 0
Solve for y in inv.: y = ±Φx, but we can simplify this to Φx since we know y
³ 0
Answer: h1(x) = Φx
|
|
(d)
|
If a(x) = |x + 3|, then function a makes a V shape.
Since a is
not one-to-one (not 1-1 in shorthand), a
is not invertible as a function.
[Remember, a function is invertible iff it is 1-1.]
Alternate explanation: Consider a value, such as 5.8, that was produced as an
output of function a. Since we
cannot determine what value of x
produced this value of a(x), a1 is not a function. Either x = 2.8 or x = 8.8; we
cannot tell.
Some values of a(x) may have unique inverses. For
example, if a(x) = 3, we can deduce that x
= 0. However, that is not good enough. All
possible y values for function a must have a unique x value associated with them in order
for function a to
have an inverse function.
|