|
M 5/1/06
|
HW due: If
you did not finish the problems that were due on Friday, then finish them.
These are all like little puzzles, and you are expected to be able to do all
of them. Remember, "x, tan x = (sin
x)/(cos x) and sin2 x
+ cos2 x = 1. From those
two facts, and from knowing which of the 6 circular functions are reciprocals
of each other, you should eventually be able to get all of the problems to
work out.
Bonus problem: If 3 chimpanzees each
type random characters (A-Z, plus space) for 6 hours per day, 4000 characters
per hour, how long will it take before the phrase “POMEGRANATE BAZOOKA” is at
least 50% likely to have appeared?
|
|
|
T 5/2/06
|
HW due:
Read §14-3 (to middle of p. 816 only) and all of §15-1; write §15-1 #14.
Also, the assignment due last Friday will be re-checked for perfection. For this one assignment only, you may
use someone else’s work if that is literally the only way you can get a clean
proof that shows all the necessary steps. Normally, that would be an honor
code violation, but for this one assignment only, you have an exemption.
Sometimes it is actually possible to learn by observing what someone else has
done. Warning: If you copy a
mistake, and the problem is spot-checked, you will not receive any credit. It
would be wise to cross-check each other’s work to make sure that there are no
errors.
|
|
|
W 5/3/06
|
HW due:
Read §15-2; write §15-1 #2, 5, 11, 17, 18.
|
|
|
Th 5/4/06
|
NSA Field Trip 8:00 a.m.–12:30 p.m. (normal dress
code) for the following students:
E period: Jack, Ken, Kevin, Khyle, Michael, Nicholas.
F period: Andrew, James, Ron, William.
Meet at the bus behind the Martin Gym (on the service road, near the gate). Bus
will depart at 8:05 sharp. I will have some minor snacks (soda and cookies),
but bring money if you wish to purchase something more from the vending
machines at the museum.
E period students not on the field trip should write up #6 on p. 917. Compare
answers with your friends, but no direct copying of work is permitted.
Note: F period will meet today as
usual, although we may start a few minutes late. You may arrive at 12:45
without penalty.
|
|
|
F 5/5/06
|
HW due:
§15-2 #2-14 even. Each problem must have
a diagram and an equation in order to earn credit. For #2 and #8, show
the full algebraic work (all steps). If you wish, you may show less work for
the rest of the problems, but a diagram and an equation are always required.
Additional HW due for E period
students who were not on the field trip: #6 on p. 917. If you are stuck,
see someone in the F period class for notes or hints.
|
|
|
M 5/8/06
|
HW due:
Please work the following buried-treasure problems. I hope you find them
interesting. Next week, if the weather is pleasant, we will go outside and
locate point X with a GPS receiver.
The latitude-longitude coordinates of the Peace Cross are N38°55'44.3",
W77°04'17.6". Suppose there is a map buried beneath the Peace Cross
(fictional, of course) that shows buried treasure at point X exactly 125 yards NNE, in the
direction of the Cathedral. You may need to consult Internet sources and/or
an encyclopedia and/or a parent to answer questions 1-13.
1. Latitude is measured in degrees north (N) or south (S) of what imaginary
line?
2. What is the maximum number of degrees of N latitude?
3. What point is at latitude S90°?
4. Longitude is measured in degrees east (E) or west (W) of what imaginary
line?
5. Through what British city does the Prime Meridian (longitude E0°0'0")
pass?
6. The International Date Line (IDL) is not a straight line. In a number of
places, it zigs and zags to avoid populated areas. However, approximately
what is the longitude of the International Date Line?
7. What is the maximum number of degrees of W longitude?
8. Washington is at approximately 77° W longitude. GMT stands for Greenwich
Mean Time. If an hour of standard time (one “time zone”) is deducted for each
15° of longitude a person travels west from Greenwich, how many time zones is
Washington behind GMT?
9. If you listen to the BBC News on WETA, you will notice that the radio
announcers occasionally state the time in GMT. If you listen to such a
broadcast on May 7, 2006, why is the GMT only 4 hours ahead of Washington
time?
10. At the Equator, each degree of longitude equals 69.39 miles. How many
feet is this?
11. At the Equator, each degree of longitude also equals 60 minutes, or 3600
seconds. How many feet are in one second of longitude at the Equator?
12. Explain why each second of longitude corresponds to considerably less
than 100 feet at Washington’s latitude.
13. By consulting a Web resource and performing some spherical geometry, I
was able to determine that at Washington’s latitude, each second of longitude
equals about 79.11 feet. However, explain why each second of latitude equals
about 101.77 feet, regardless of where you happen to be in the world.
Now answer these questions on your own:
14. Sketch a treasure map that places the Peace Cross at the origin. Let the x-axis be the east-west axis, and let
the y-axis be the north-south axis.
Mark a point X that is 125 yards
(375 feet) from the origin and in a direction approximately NNE of the
origin.
15. If E is 0° and N is 90°, compute the angle for NE (______ °) and NNE
(______ °). Note: NNE
(north-northeast) is halfway between NE and N.
16. Use trigonometry to find the (x,
y) coordinates of X in feet. Remember, the Peace Cross
is (0, 0). Show your work, and give answers to 3 decimal places.
17. Using the conversion factors of 101.77 feet per second of latitude and
79.11 feet per second of longitude, compute the lat-long coordinates for X, to the nearest tenth of a second.
Show your work.
18. Use the Law of Cosines to show that if the earth can be considered to be
a sphere of radius R = 6400 km
(3975.76 mi), then the radius r of
the circle of latitude that passes through the Peace Cross is slightly less
than 5000 km. Proceed as follows:
(a) Define points as follows: C =
center of the earth, N = North
Pole, and P = Peace Cross. Let d = NP be the straight-line distance (not the great circle distance)
from the North Pole to the Peace Cross, following an imaginary tunnel through
the earth. Make a 3-dimensional sketch and compute d by the Law of Cosines. Show your work. Hint: DPCN is isosceles, and ÐPCN can be determined (if you think about it
carefully) by knowing the latitude of the Peace Cross. This problem may
require anywhere from 2 minutes to 20 minutes, depending on how well you are
able to focus your thoughts. I guarantee that you cannot do this while
listening to an iPod. You must THINK!
Send me an e-mail if you are stuck. No e-mail, no credit.
(b) Let q be the angle formed by
segment NP and the earth’s axis of
rotation. Use the Law of Cosines a second time to compute q. Show your work. If you are proficient with the Law
of Cosines, you can probably do part (b) even while listening to an iPod,
since after you have found d, you
know the lengths of all 3 sides of DPCN.
(c) Now use simple trigonometry to find r.
You can turn the iPod on and maybe even chat on the phone with somebody while
answering this part.
19. Challenge Bonus Problem
(expected of all honors-track hopefuls): Let R = 6400 km = radius of the earth. Without using your calculator,
explain why r = R cos(38°55'44.3") in #18. This
problem is easier than #18 if you look at it the right way.
|
|
|
T 5/9/06
|
HW due:
§15-9 #3, 5. These are both fairly good “real world” problems of the type
that you can expect to see on Friday’s test. Also finish yesterday’s
problems, using the sketch and hints that were given in class yesterday. One
or both of these assignments will probably be collected.
Here is a complete solution to #4, which is quite similar to #3. See if you
can adapt the ideas.
4. Let X be the vertex of the 15°
angle, let Y be the vertex of the
29° angle, let C be the vertex of
the right angle (closest approach point), and let B be the buoy. XY =
1300 m (given). Let YC = x, an independent variable that we
will adjust with our calculator. Let XB
= c, the hypotenuse of the large
right triangle. Let YB = r, the hypotenuse of the small right
triangle. Let CB = d, the distance from the boat’s path
to the buoy.
By Pythag. Thm., (1300 + x)2
+ d2 = c2, but since d = x tan 29°, we can rewrite this equation as c2 = (1300 + x)2
+ (x tan 29°)2, which
gives c2 as a function
of x alone.
By looking at DXCB and focusing on the fact that cos 15° = (1300 + x)/c,
we see that c = (1300 + x)/(cos 15°), which gives c as a function of x alone. Substitute this value for c
into the equation above to get a single equation involving the unknown x, namely this:
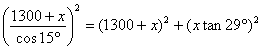
Now, this equation is “merely” a quadratic in x, which can be solved by the quadratic formula. However, the
algebra is tedious. By using guess-and-check you can see that a value of
about 1200 for x seems to satisfy
the equation. A better way is to set Y1 on your calculator to be
the LHS of the equation and Y2 to be the RHS. Plot both functions
in a suitable window, using [0, 2000] as your domain and ZOOM 0 to find the
window. Use the intersection finder (2nd CALC 5) to see where the functions
cross. The X value, namely 1216.4203 . . ., is what we called x above. From this it is easy to
answer all the questions.
(a) r = x/(cos 29°) » 1390.799 m
(b) d = x tan 29° » 674.273 m
(c) x » 1216.420 m
(d) supplement of arctan(d/(7000 – x)) » supplement of arctan(0.11658 . . .) » 173°21'.
Problem #3 is similar but somewhat easier because there are fewer questions
to answer.
|
|
|
W 5/10/06
|
HW due:
Read pp. 745-748 and work the following review problems:
p. 798 #T1 all, T2 all, T3b.
p. 859 #R1ab, R2ab
p. 879 #3, 9, 11
#18abc from Monday’s assignment (a and b are Law of Cosines review, c is trig
review)
Compute the probability that Mr. Hansen sinks at least one free throw in 9
attempts. (Mr. Hansen is a 22% free-throw shooter, and you may assume that
this probability is the same for each attempt, i.e., that the trials are
independent.)
Compute the number of left-to-right arrangements of king-ace full houses (3
kings and 2 aces, or 2 aces and 3 kings) using a standard deck of cards.
If Monday’s assignment is collected again, it will be a double scan this
time. Remember to use the method we discussed in class for cross-checking
your answer to #18b.
In class: Review for Friday’s test.
|
|
|
Th 5/11/06
|
NSA Field Trip 8:00 a.m.–12:30 p.m. (normal dress
code) for the following students:
E period: Ken.
F period: Francis, Sam.
Meet at the bus behind the Martin Gym (on the service road, near the gate).
Bus will depart at 8:05 sharp. I will have some minor snacks (soda and
cookies), but bring money if you wish to purchase something more from the
vending machines at the museum.
All students not on the field trip should write up #7 on p. 917. Compare
answers with your friends, but no direct copying of work is permitted.
Note: Because we went significantly
overtime on Wednesday, F period will not meet today. Use the class period for
study and review. If you were not on the field trip, remember that there is
an additional HW problem due tomorrow.
|
|
|
Study Help
|
Answers to the review problems due W 5/10
are now available.
|
|
|
F 5/12/06
|
HW due: p.
917 #7. Those who attended the field trip yesterday are exempt, but it is a
good review problem that is worth working if you have the time. It is
possible that a simplified version of this problem could appear on the test.
Test on Probability, Trigonometry, Circular Functions, Identities, and Law of
Cosines. Problems will be similar to the review problems due Wednesday.
Two additional types of “without calculator” problems may be seen on this
test:
1. A problem similar to #1-14 on p. 749.
2. A problem similar to #1-14 on pp. 752-755.
The formula y = C + A cos (B(x – D)) from the middle of p. 745 will be furnished for you on the
test. You do not need to memorize it. However, the meanings of parameters A, B,
C, and D, as well as the skill of working with them correctly, must be
stored in your brain.
|
|
|
M 5/15/06
|
No additional HW due.
|
|
|
T 5/16/06
|
HW due:
pp. 555 #R1, R2 all, R3abcd, R4 all (without calculator—make only a rough
sketch), R6; pp. 552-553 #5. Also spend a few minutes reminding yourself how to
recognize and/or prove evenness or oddness in functions. Evenness means
symmetry about the y-axis, since f (–x) always equals f (x). Oddness means symmetry about the
origin, since f (–x) always equals –f (x).
|
|
|
Study Help
|
Here are some additional solutions
to help you prepare for tomorrow’s test.
R3b. Use the trick of writing the factored form (x – root1)(x – root2) =
0. You have been doing this for years with simple problems like (x – 7)(x – 8) = 0, for which the roots are obviously 7 and 8. How about
using some complex roots that are a little more advanced than 7 and 8? Our
roots are 3 + 4i and 3 – 4i. (We know that, because if a
polynomial has real coefficients, then the complex roots, if any, must always
occur in conjugate pairs.) Therefore, we multiply (x – (3 + 4i))(x – (3 – 4i)) = 0. We “FOIL” the left side to get x2 – (3 – 4i)x – (3 + 4i)x + (3 + 4i)(3 – 4i) = 0. After simplifying (2 or 3 more steps), we get x2 – 6x + 25 = 0, which is the final answer.
R3c. By the quadratic formula, the roots are (4 ± Ö(16 – 20))/2 = 2 ± i. Use the trick of the
previous problem to write the factored form as (x – (2 + i))(x – (2 – i)). I will accept the answer in that form, or you can rewrite it
as (x – 2 – i)(x – 2 + i).
R3d. To find the roots, set 25x2
+ 1 = 0. That means x2 =
–1/25, which means x = ±i/5 are the roots. You might proceed as in the last
two problems to write (x – i/5)(x + i/5), but that is
not correct, since the “FOIL” would only give x2 as the leading term. Clearly, you need to multiply
through by 25, or more properly by 5 on each term, in order to get 25x2 as the leading term.
Final answer: (5x – i)(5x + i).
R4a. The student who did this on the board did not follow instructions.
“Synthetic substitution” means to use the technique of synthetic division.
(The two processes are equivalent, thanks to the Remainder Theorem. By the
way, you should know the statement of the Remainder Theorem for tomorrow’s
test.) Here is the proper technique:
2 | 5 –11
8 9
|_____10__–2__12___
5
–1 6 21
Conclusion: (5x3 – 11x2 + 8x + 9) divided by (x –
2) equals (5x2 – x + 6) + 21/(x – 2). In other words, the remainder is 21. By the Remainder
Theorem, the remainder of 21 also equals P(2).
R4c. If you know a root (in this case, 2 is an easy root to find), you simply
divide the polynomial by (x –
root). Here is the technique:
2 | –2 –1
6 8
|_____–4 –10 –8___
–2
–5 –4 0
The remainder is 0, which tells us that (–2x3 – x2
+ 6x + 8) divided by (x – 2) equals (–2x2 – 5x – 4)
exactly. Use the quadratic formula on (–2x2
– 5x – 4) to get the remaining two
roots, both of which are complex. The student who did this problem on the
board stopped with only the real root of 2, which is of course much too soon.
Final answer: S = {2, –5/4 + i(Ö7)/4, –5/4 – i(Ö7)/4}.
R4d. Here is the technique. Remember to use placeholders of 0 for the powers
of x that are not present.
–2 | 1 0
0 17
|____–2 4
–8___
1
–2 4 9
Answer: The remainder is 9.
R4e. Remember, a quartic function has at most 3 “wiggles.” Thus, it could
look like a U, an upside-down U, a rounded M, or a rounded W. The shape that
does the job is a rounded M.
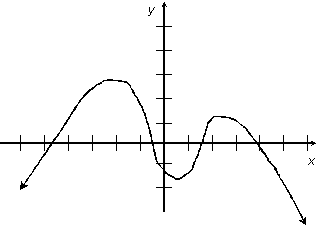
Don’t forget to review evenness and oddness also. Good luck tomorrow!
(Actually, luck has nothing to do with it. Careful study and reflection are
the key.)
|
|
|
W 5/17/06
|
Test on Evenness, Oddness, and Chapter 10 (omitting
§10-5).
|
|
|
Th
5/18/06
|
[See continuation on main Algebra II Zone page.]
|
|
|
F
5/19/06
|
Last day of fourth quarter.
|
|
|
|
Exams (schedule TBA).
|
|
