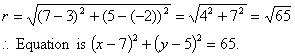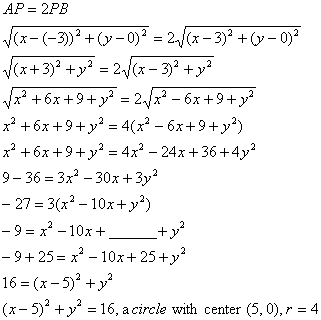Monthly Schedule

(Algebra II, Periods E and F)

W 2/1/06

HW due: §8-6 #4, 9, 10. All problems should be complete now.

 

Th 2/2/06

HW due: p. 453 #R1-R3 all, R4b; pp. 454-455 #T1-T7 all, §8-6 #11, 12.

In class: Review.

 

F 2/3/06

Test on Chapter 8. Extra-time students need to take the first segment from 7:30 to 7:50 a.m. in Room R. Everyone else will have a full Friday period (40 minutes) to take the test.

Solution to §8-6 #12:

(pre-a) Let F = force (newtons)
                   P = pressure (newtons/m2)
                   A = area (m2)
                   l = length of room (m)
                   w = width of room (m)
(a) Fexerted = PA
(b) Fwithstandable = k1(2l + 2w)
(c) A = k2(2l + 2w)2
(d) From (c), we can solve for perimeter to get 2l + 2w = (A/k2)0.5.
      Therefore, equation (b) becomes Fwithstandable = k1(A/k2)0.5 = k3A0.5, where k3 is a constant
      formed by combining k1 and k2.
(e) If Fexerted = Fwithstandable, then Fexerted = PA = k3A0.5 by transitivity.
      Solve for P to get P = k3A0.5/A = k3A–0.5, which is the same as saying that
      P varies inversely with the square root of A.
(f) Let A1 = area of first roof, A2 = area of second roof.
      Similarly, let P1 = critical pressure for first roof, P2 = critical pressure for second roof.
      Since A1 = 9A2, we have P1 = k3A1–0.5 = k3(9A2)–0.5 = 9–0.5k3A2–0.5 = 9–0.5P2. Since
      9–0.5 = 1/3, we conclude that the first roof’s critcal pressure is 1/3 as large as the
      second roof’s critical pressure.
(g) One would want the room with the greatest critical pressure, i.e., the smallest possible
      roof area. A closet would serve well. However, it should be an interior closet, since
      otherwise the tornadic winds whipping around the house could cause debris impaction
      and destruction from the outside.

 

M 2/6/06

HW due: Read §§9-1 and 9-2; write §9-2 #4, 13-19 all. This is a nice short problem set for the Super Bowl weekend. Problem #4 should take about 5 minutes if you know what you are doing, and #13-19 should take about 1 minute each. One of them has been done for you as an example:

13. Center at (7, 5), containing (3, –2).
Answer:

 

T 2/7/06

HW due: Read §9-3; write §9-3 #Q1-Q9 all. We will do the actual problems in this section after we have had a chance to discuss the reading as a class.

 

W 2/8/06

HW due: Use a string, a pencil, a piece of cardboard, and two thumbtacks to make a good-quality ellipse. Label the foci (i.e., thumbtack points) as F1 and F2. Label the major axis as segment AD, the minor axis as segment BE, and the center as C. Also answer the following questions:

§9-3 #18.
20. Find in an encyclopedia or other reference source a formula for the area of an ellipse, and calculate the area of your ellipse. Show your work: formula, plug-ins, and answer.

 

Th 2/9/06

HW due: Read §9-4 twice; write §9-3 #15, 16.

 

F 2/10/06

HW due: Write §9-3 #6-8 all, §9-4 #7, 8, 18.

 

M 2/13/06

HW due: pp. 485-486 #Q1-Q10 all, plus the following review questions from Friday’s video and discussion that followed. (If you missed class, contact a classmate for the notes.)

R1. What secret society of mathematicians did Donald disdain because it consisted of “eggheads”?
R2. What was the symbol of that secret society?
R3. Who ultimately prevailed in the three-cushion billiard competition, Donald or “the spirit”?
R4. What sequence demonstrated by Mr. Hansen is related to the Golden Ratio?
R5. What does the sequence in question #R4 have to do with pine cones?
R6. What conic section was not demonstrated in the video?
R7. How do we slice a cone to achieve a degenerate form of the answer to #R6?

 

T 2/14/06

HW due: Read §9-5; write §9-5 #Q1-Q10 all, 8, 4, 6. Hint: If you can’t understand how to do #4 and #6 using the book’s method, interchange the roles of x and y and treat them like #8. Then make a mirror image across the line y = x. (Why does this work?)

 

W 2/15/06

HW due: §9-5 #2, 5; §9-6 #2, 4, 8.

Below is a completely worked example for §9-6 #1 to show you the correct approach in §9-6. Notice that you will be using the distance formula each time. (If you don’t remember how to use the distance formula, or if you don’t remember how to solve radical equations, you will need to re-learn those techniques now.)

1. The locus is given to be in a plane (see introductory paragraph for problems 1-12) and is described as follows: “For each point [in the locus], its distance from the fixed point (–3, 0) is twice its distance from the fixed point (3, 0).”

Let P(x, y) denote a point somewhere in the locus (wlog). Let A be the point (–3, 0), and let B be the point (3, 0). Then our locus can be described as the set of points P in a plane such that AP = 2PB.

Since we have expressions for the coordinates of points A, B, and P, we can apply the distance formula and can then solve the radical equation that occurs. Here are the steps:

 

Th 2/16/06

HW due: Read §9-8 (mostly a review of last year’s geometry class); write §9-8 #1, 3, 7.

 

F 2/17/06

No school (teacher professional day).

 

M 2/20/06

No school (holiday).

 

T 2/21/06

HW due (E period only): Read §9-7; write §9-7 #5. F period is exempt from this assignment, since we did it in class.

After school: Big Trig competition.

 

W 2/22/06

Oops! I got so distracted by the Big Trig competition that I forgot to post your assignment. By the rules, you have a night off with no homework. However, you can productively start reading in Chapter 10, or you can work on some of the Mathcross puzzles.

 

Th 2/23/06

HW due: In §9-8, do #18-26 all (identifying the figures only), plus any 3 of your choice done completely. For example, for #17 your identification step would be to write, “hyperbola, hyperbola.” For the 3 that you do completely, show sketch, all algebra, the solution set, and the check. You are encouraged to use your calculator at the end, as a check, but the writeups need to be complete.

Warning: You have a test coming up. If I were you, I would choose problems that tested parabolas, hyperbolas, ellipses, and lines. I would not choose the 3 easiest problems I could find.

 

F 2/24/06

Test on Chapter 9.

 

M 2/27/06

HW due: Read the notes below; write §10-2 #3-30 mo3, 35-38 all, 42, 43. If you have forgotten how complex numbers work, you may wish to reread some of the information in §10-2, but that is optional.

Note concerning |z|: The notation |z|, which we read as “modulus of z,” refers to the distance from the origin. In this respect, it is a generalization of the concept of absolute value. For example, if z = 7 – 24i, then the distance from the origin is (by the distance formula), the square root of (72 + 242), or simply 25.

Special bonus fact: , where we use the notation  to mean the complex conjugate. For example, if z = 7 – 24i, then  = 7 + 24i, and
 = 625. Is the square root of that equal to 25? Why, yes, it is! Wasn’t that fun? This gives us an easy way to find the modulus of any complex number.

 

T 2/28/06

E period will meet at the usual time today for Form III and V. Form IV students in both E and F period will be watching Romeo and Juliet.

HW due for everybody: Work on Monday’s and Wednesday’s assignments. Wednesday’s assignment will take you about double the usual 35 minutes.

 

 

Return to the Algebra II Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 01 Mar 2006