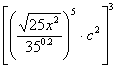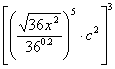|
T 11/1/05
|
HW due:
§5-7 #6, 7. You may use QuadReg to check your particular equations, but for
credit you must show the 3-equation setup that helps you employ the rref
procedure. That’s right; answers without the 3-equation setup will not count.
|
|
|
W 11/2/05
|
HW due:
§5-7 #17, 18. Also study for your quiz.
Today’s Quiz will cover all of
Chapter 5 except for §5-6. I will be on a field trip today, and you will have
a substitute teacher.
|
|
|
Th 11/3/05
|
HW due:
Read §§6-1 and 6-2; write §6-2 #1-13 odd, 15-17 all. Note: The key that your textbook refers to as the yx key is actually the ^
key (just above the division symbol).
|
|
|
F 11/4/05
|
No school.
|
|
|
M 11/7/05
|
HW due:
Read §6-3; write §6-3 #11-32 all, 40. For #21-26, write down the number that
your calculator gives you for the left side of the equation, as well as the
number your calculator gives you for the right side of the equation. (They
should be equal.)
|
|
|
T 11/8/05
|
HW due:
Read §6-4; write §6-4 #2-46 even, plus the following additional problems:
48. Estimate 328 without using a calculator.
50. Estimate 6018 without using a calculator.
52. Estimate 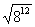 without using a
calculator. without using a
calculator.
|
|
|
W 11/9/05
|
HW due:
Finish yesterday’s assignment, including the 3 supplementary problems. Then
do the following 3 problems.
1. Which is larger, 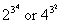 ? Show your work. (Do not use a calculator.) ? Show your work. (Do not use a calculator.)
2. Create another problem similar to #50 or #52, using your own imagination,
and write out your estimation steps with
a reason for each step. For a bonus point, do a second method for the
same problem. Be sure to distinguish between the equals sign (=) and the
approximately-equals sign (»). An example is shown below.
Example with reasons:
3045 = (2 · 15)45 by substitution
= 245 · 1545
by distrib.
= (220)(220)(25)(1545)
by PRAE
» (1 million)(1 million)(32)(1545) by
subst. and rule that 210 » 103
» (106)2(32)(1645)
by subst. and estimating 15 » 16
= (1012)(32)(1645)
by PPME
= 32 · 1012 · (24)45
by commut. and subst.
= 32 · 1012
· 2180 by PPME
= 32 · 1012
· (210)18 by PPME
» 32 · 1012 · (103)18
by subst. and rule that 210 » 103
= 32 · 1012
· 1054 by PPME
= 32 · 1066 by
PRAE
= 3.2 · 1067
in scientific notation (divide first part by 10, increase exponent by 1).
Note that this final estimate is too large by a factor of about 10, but that
is a discrepancy of only 1 order of magnitude compared to the real answer.
With numbers this huge, anything within a factor of 100 (i.e., 2 orders of
magnitude) is certainly acceptable.
Example (another method):
3045 = (3 · 10)45 by substitution
= 345 · 1045
by distrib.
= 3 · 344 ·
1045 by PRAE
= 3 · (32)22
· 1045 by PPME
= 3 · 922 ·
1045 by PPME
» 3 · 1022 · 1045 by subst. and
estimating 9 » 10
= 3 · 1067
by PRAE
This is easier that the first method but also produces an answer that is
about 1 order of magnitude too large.
3. Estimate the mass of the earth, using the following ground rules (no pun
intended) agreed to by the E period class:
(a) The earth’s volume is approximately equivalent to a cube 10,000 km on a
side.
(b) One km = 1000 m = 103 m = 103 (100 cm) = 103
(102 cm) = 105 cm.
(c) One cm3 of earth has a mass of about 5 g, since our planet is
about 5 times denser than water on average.
|
|
|
Th 11/10/05
|
HW due:
§6-6 #3-39 mo3, 57-60 all, 66-70 even. Then, complete as much of the STA Mathcross #1 as possible. You may seek
help from your classmates, from your parents, and from the Internet, but not
from students of mine in other classes. There will be a prize for the best
entry.
|
|
|
F 11/11/05
|
HW due:
Read §6-7; write §6-7 #3-8 all. (Use guess-and-check or 2nd CALC intersect.
Write a solution set in each case.)
|
|
|
M 11/14/05
|
HW due:
Read §§6-8 and 6-9; write §6-9 #1-30 all. You may find it easier to do them
out of order, with #13-30 followed by #1-12. The first three of each group are
done below as examples. (You need to do them as part of your HW, but you may
follow the work below if you wish.)
13. log4 16 = log4 (42) = 2
Calc. check: log(16)/log(4) = 2ü
14. log3 81 = log3 (92) = log3 (32)2
= log3 34 = 4
Calc. check: log(81)/log(3) = 4ü
15. log3 (1/9) = log3 (1/32) = log3
3–2 = –2
Calc. check: log(1/9)/log(3) = –2ü
1. log2 x = 3
In English: “The base-2 log of what number
equals 3?”
Note to self: “A logarithm is always an
exponent, according to blue box on p. 269.”
Internal thought: “The equation says that the
logarithm for x equals 3.”
Analysis: “The equation really says that the exponent for x equals 3.”
Nearly complete thought: “The base, 2, raised
to the exponent, 3, must equal x.”
Conclusion: x
= 8.
Calc. check: log2 x = log2 8 = log(8)/log(2)
= 3ü
2. log3 x = 2
In English: “The base-3 log of what number
equals 2?”
Note to self: “A logarithm is always an
exponent, according to blue box on p. 269.”
Internal thought: “The equation says that the
logarithm for x equals 2.”
Analysis: “The equation really says that the exponent for x equals 2.”
Nearly complete thought: “The base, 3, raised
to the exponent, 2, must equal x.”
Conclusion: x
= 9.
Calc. check: log3 x = log3 9 = log(9)/log(3)
= 2ü
3. log3 x = 3
In English: “The base-3 log of what number
equals 3?”
Note to self: “A logarithm is always an
exponent, according to blue box on p. 269.”
Internal thought: “The equation says that the
logarithm for x equals 3.”
Analysis: “The equation really says that the exponent for x equals 3.”
Nearly complete thought: “The base, 3, raised
to the exponent, 3, must equal x.”
Conclusion: x
= 27.
Calc. check: log3 x = log3 27 =
log(27)/log(3) = 3ü
|
|
|
T 11/15/05
|
HW due:
Read §6-10; write §6-10 #9-42 mo3, 31, 32. For #9-30, please round off the
values to log 2 » .3, log 3 » .5, and log 5 » .7.
|
|
|
W 11/16/05
|
HW due: Read
§6-11; write §6-11 #1-10 all; then compute 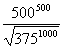 ; ;
finally, use #27 to prove #30. In other words, assuming that #27 is true,
prove that #30 must also be true. A proof of #27 is shown below.
Given: x > 0, a > 0, a ¹ 1
Prove: loga x = (logb x)/(logb
a), where b is any legal base (b
> 0, b ¹ 1)
Note: In practice, we almost always
take b = 10 so that we can apply
this formula by using the “LOG” key on the calculator.
Proof: Since loga x is unknown, let y = loga x. We will solve for y indirectly.
First, rewrite as
an exponential equation: ay
= x.
Then, take logs
of both sides, using the base-b
logarithm (where b > 0, b ¹ 0).
Result so far:
logb ay = logb x.
Now apply
property 3 from p. 276, the “pull it down” property.
Result: y logb a = logb x.
Finally, divide
both sides of this equation to solve for y.
Result: y = (logb x)/(logb
a). (Q.E.D.)
|
|
|
Th 11/17/05
|
HW due:
§6-11 #27, 28, 29. Try to do #27 several times until you can do it reliably
without looking at your notes, since you will be required to do #27 from
memory on your next test. Then do the following additional problems.
1. Compute 700700. (Give answer in scientific notation.)
2. Compute the square root of your previous answer.
If you are up to a real challenge, try the STA
Mathcross #1 or STA Mathcross #2.
|
|
|
F 11/18/05
|
Test on §§5-6 through §6-11 (pp. 200-289). Note that although we did not do any problems in
§6-8 yet, there is nothing unusual or exciting there. For example, here is
how you would solve a problem like #22 on p. 268:
22. 73x = 10000
Rewrite as 3x = log7 10000.
Apply change of base: 3x = (log 10000)/(log 7).
Simplify: 3x = 4/(log 7).
Solve for x to get x = 4/(3
log 7).
If a decimal approximation had been
requested, then you would write 1.578.
Review of properties of logarithms (see p. 276):
1. LPSL: The log of a product equals the sum of the logs.
2. LQDL: The log of a quotient equals the difference of the logs.
3. “House Rule”: The log of a power allows you to pull the power down and
multiply.
|
|
|
Weekend
|
Review the test you took on Friday and the solution key. The last problem was as follows:
E period: 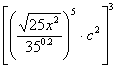
F period: 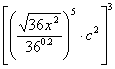
If you wish to know your approximate score, please send me an e-mail.
|
|
|
M 11/21/05
|
Another Test on §§5-6 through §6-11 (pp. 200-289). The higher of the two scores (last Friday and
today) will be recorded. If you are happy with how you did last Friday, then
you can enjoy a restful weekend with no work. If you are not happy with how
you did last Friday, then resolve to do better today. Attendance is required
at both classes for everyone.
|
|
|
T 11/22/05
|
HW due:
Read §6-12; write §6-12 #17-26 all. Remember how we evaluated f (g(x)) previously, by starting with g(x)
and then applying the “f function
machine” to it. If the final result is simply x, then apparently f is
the inverse of g, correct?
|
|
|
|
Thanksgiving break.
|
|
|
M 11/28/05
|
No additional HW due. However,
equipment checks and spot checks of old HW assignments may occur. Remember
that the quality standard for a “4” on a previous assignment, such as the
§6-12 assignment due last Tuesday, includes writing out the setup for each
problem.
|
|
|
T 11/29/05
|
HW due:
§6-12 #1-16 all. Reword part (a) to read “Find an equation for the inverse
relation,” since some of the inverses are not functions. Also, be sure to
label very clearly which parts of your answer refer to the original function
and which refer to the inverse. For example, here is how you would answer #5:
5.(a) Fcn.: y = 0.1x2
Inv.: x = 0.1y2
y2 = 10x
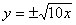
(b) [Show a rough sketch, with the y = x line of symmetry
as a dotted line. You may use
your calculator to assist
you, but remember that it cannot plot all inverses correctly.]
(c) Inv. is not a fcn.
|
|
|
W 11/30/05
|
HW due:
Correct last night’s HW to 100% and answer review questions R2, R3cd, R4d,
R5d, R9, R10, and R12 on pp. 318-319.
In class: Review.
|
|