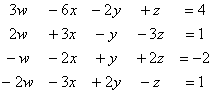Monthly Schedule

(Algebra II, Periods E and F)

M 10/3/05

HW due: Read §§4-1 and 4-2. You should find that this is all a review of material learned in previous courses. Then write §4-2 #2, 22. You will notice that #2 is quite easy, and #22 is quite challenging. For each problem, you must check your (x, y) ordered pair in both equations, in writing. No credit if you did not show (in writing) the process of checking your solution against the original equations. Use the “question mark equal sign” during your checking, as we have discussed in class.

Write solution in the following format:

S = {(x, y)}

For example, if after doing all your algebra, you determine that x = 3.4 and y = –4.1, then you would write your answer as follows:

S = {(3.4, –4.1)}

Note that both curly braces and parentheses are required. Here is how we would read that line:

“The solution set equals the set consisting of the ordered pair (3.4, –4.1).”

 

T 10/4/05

HW due: Read §4-3; write §4-3 #1, 2, 4, 6. A “show it” check or calculator check (your choice) is required for each one. If you use a calculator check, write “calc. check OK” or some similar words to that effect.

 

W 10/5/05

HW due: Read §4-4; write §4-2 #27-30 all (calculator permitted). For tonight only, you need not show your work. However, you must check your answers, using either a “show it” check or a calculator check.

Quiz possible (10 pts.) on linear systems and determinants. You may use your calculator as a check, but work will be required for full credit.

 

Th 10/6/05

HW due: Read §4-6; write §4-6 #1-14 all (using calculator).

 

F 10/7/05

No school.

 

M 10/10/05

No school.

 

T 10/11/05

HW due: §4-7 #11-18 all (see note below); §4-8 #13, 14, 17. There is no need to show work. Provide written-out “show it” checks only for the odd-numbered problems. However, each answer must be shown as a solution set, and in the event that your system has infinitely many solutions, you will need to use a format such as S = {(x, y, z): x = 15 – 2z, y = 6.5 + z/4, z Î Â}. Checking such a solution is difficult, but it is good algebra practice.

Note: When you obtain the result of your rref([A]) operation that includes “messy” decimals, immediately push the MATH button on your calculator and press ENTER twice in order to perform a „Frac conversion. That way, you will see the numbers displayed as fractions instead.

 

W 10/12/05

HW due: §4-8 #17 (using Cramer’s Rule); §4-9 #1-4 all (using Cramer’s Rule). Only the setups are required. Show the determinants using the correct vertical bar notation. You may save writing by defining how the denominator determinant is found, since you can than re-use the value as a symbol instead of having to rewrite the entire thing.

Note: Answers without correct setups will not qualify for points. In fact, answers are not required at all.

Although it is not required for points, I would like you to use the det() function (MATRIX MATH 1) to verify that at least one of these problems works out to match the rref() results.

 

Th 10/13/05

HW due: §4-10 #4-16 mo4. There is no need for reading notes tonight, since this material is a review from last year. However, as you know, reading notes are normally required each night.

 

F 10/14/05

Test on Chapters 3 and 4. Suggested study materials include the review problems and practice tests at the end of each chapter. On some of the problems, you will not be permitted to use your calculator.

 

M 10/17/05

Calculator Quiz on Linear Systems (10 points).

It has been suggested to me that this would be a good time for a weekend of no homework. That sounds like a good idea. However, if you were one of the people who spent way too long on problem #1 on Friday’s test (anything over 4 minutes is way too long), then I strongly suggest that you practice repeatedly on the problem below until you can do the whole thing from beginning to end in less than 2 minutes. That means doing all of the following:

  • Enter a fresh matrix.
  • Perform the rref operation.
  • Punch MATH ENTER ENTER to convert to fractions.
  • Write the solution set legibly on a piece of paper. By the way, the solution set to the problem given below is S = {(–10/7, –5/7, –18/7, –8/7)}.

 

Can you do all 4 steps in under 2 minutes? I tried several times, and my best time was 1 minute and 13 seconds. My average time was almost exactly 1½ minutes, and that includes double-checking the data entry for accuracy!

Now you may say, “But of course you can do it in under 2 minutes, Mr. Hansen. You’re the teacher.” Well, gentlemen, superior math experience has nothing to do with it. In fact, judging by how adept you are at punching cell phone buttons and video game buttons, I’m amazed that I, a middle-aged man, can compete with you at all. You should be as fast as I am (or faster) in this calculator skill.

You can surely find other practice problems, either by taking them from the textbook or by inventing problems for each other as a contest. However, here is the linear system I used for practice:







For your quiz today, you will have exactly 4 minutes (6 minutes if you have a learning issue that qualifies you for extended time). That’s all!

 

T 10/18/05

HW due: Write §4-4 #2-26 even. Then use the Dep-Scribble-SWYK-EA procedure to answer §4-4 #29.

Here is how you should show “adequate work” for #2 and #13, shown here as examples:

2. g(5) = 52 + 5 + 1 = 31
13. f (g(0)) = f (02 + 0 + 1) = f (1) = 3(1) + 11 = 14

 

W 10/19/05

HW due: Read §§5-1 and 5-2; write §5-1 #1-6 all, §5-2 #1-8 all, 13-18 all. An example problem is worked below:

7. x2 – 13x + _______
Take coefficient of middle term (–13), divide by 2, and square. Answer: (–13/2)2 = 169/4.

Bonus Fun HW (2 pts.): Store 2.5 into the variable A on your calculator (2.5®A ENTER), 0.7 into the variable X (.7®X ENTER), and iterate the command AX(1–X)®X until you can see what the long-term behavior is. You can think of this as an iterated function f where f (x) = ax(1 – x). Then repeat the experiment using 2.6 for A, then using 2.8 for A. What do you predict the long-term behavior will be if A=3? What if A=4? Record all your results and predictions in a table.

 

Th 10/20/05

HW due: Write §5-3 #3-33 mo3.

 

F 10/21/05

HW due: Write §5-4 #2-6 even, plus write out the entire proof of the quadratic formula, step by step, with an explanation for each step. Start with 0 = ax2 + bx + c with arbitrary parameters a, b, c Î Â, a ¹ 0. If at all possible, try to do what I did when I was your age, working without consulting your notes. The process is painful, but believe me, after you have survived it, nothing involving quadratics will ever frighten you.

 

M 10/24/05

HW due: Read §5-5; write §5-4 #14, 16, 18, 20, 25, §5-5 #1.

 

T 10/25/05

HW due: §5-5 #2-14 all. Use your calculator to check all answers, and perform written checks for #5b and #6d.

 

W 10/26/05

HW due: Review problems. Demonstrate to me that you have performed a substantive review. For example, you could show work toward most or all of the problems mentioned in tomorrow’s calendar entry.

In class: Review. Here is a blank copy of the F period version of the previous test to help you study. An answer key is also available.

 

Th 10/27/05

Cumulative Test Through §5-5. Questions will come primarily from Chapter 5. However, you should be able to answer any of the review questions on pp. 224-227 except for #4, 8, 9. Also, you need to know the quadratic formula by heart. Although you do not need to memorize every step of the proof of the quadratic formula, you need to be able to provide a reason for each step in the proof.

The format of the test will be mostly short answer (matching, multiple choice, and fill-in-the-blank). There will be little or no partial credit. After you have worked through the book’s review questions and have reread any portions of the text that you may have forgotten, you should work on these additional review questions. An answer key is available, but please do not peek until you have written out the answers.

 

F 10/28/05

No additional HW due today. Some old HW may be checked, however.

Last day of first quarter. In class: Ask-Backward Bingo.

 

M 10/31/05

HW due: §5-7 #3, 5. Before solving for a, b, and c in your quadratic function, be sure to write out the simplified system of linear equations that involve a, b, and c. I will expect to see this step for full credit. However, this will also help you, since it is much easier to punch in the matrix correctly if you are working from your written notes than if you are trying to do all the work in your head.

 

 

Return to the Algebra II Zone

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 08 Nov 2005