|
1.
|
As the number of trials increases,
the sample proportion of successes approaches the true probability of the
event. (Alternate form: As the number of trials increases, the sample mean approaches the true mean of a population.)
Note that it is assumed that trials are independent. If you prefer to use
mathematical notation, LOLN may be stated as 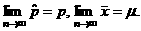
Here are paraphrased versions of some of the incorrect answers I saw:
“As the number of trials increases, the probability
approaches the relative frequency.”
[Wrong since probability doesn’t approach anything.
Probability already is something,
namely the long-run relative frequency of success. The student meant to say
that the sample proportion
approaches something.]
“The event approaches the true probability.”
[Wrong since “event” is not a number; it is an event. The sample proportion of the event—or you
could say the observed proportion of successes—is approaching the true
probability.]
“The long-run relative frequency approaches the observed
sample proportion.”
[Wrong; stated backwards.]
“In the long run, the long-run relative frequency
approaches the probability.”
[Essentially correct, but circular, since “long-run
relative frequency” is already defined to equal probability. It would be better
to say, “In the long run, the observed
relative frequency approaches the probability.” Now, you could respond by
saying that that statement is also circular, and guess what? You would be
right. LOLN is, at its root, nothing more than a tautology, by which we mean a statement that
is self-evidently true by virtue of how the ground rules have been set up. In
this case, the ground rule—namely the definition of probability as long-run
relative frequency—forces the LOLN to be true.]
|
|
2.
|
250, since the trials are
independent
Explanation: LOLN makes no attempt to “settle the score” or “even things
out.” Instead, the imbalance that may be present in any initial short run
(and by convention, any finite sample is considered to be a short run) tends
to be diluted by the later trials. Interestingly, although the percentage error tends to zero in the
long run, the expected size of the absolute error keeps growing and growing
as the sample size increases!
You may ask, “Mr. Hansen, are you saying that if I flip a fair coin 1 million
times, the absolute discrepancy between the head count and the tail count
will probably be greater than if I flipped the same coin only 1,000 times?”
The answer is yes! However, the relative error (i.e., the percentage difference
between the observed head proportion and .5) will almost certainly be
smaller.
|
|
3.
|
P(ace) = 4/52 = 1/13
P(ace | club) = 1/13, since there
are 13 clubs, one of which is an ace
Since the probability of ace is unchanged by the additional information of
having a club, the events are independent.
Although P(ace
| club) = 1/13 can certainly be calculated by common sense, you may also use
the conditional probability formula:
P(ace | club) = P(ace Ç club) / P(club)
= P(ace of clubs) / P(clubs) = (1/52)/(13/52) = 1/13.
Note that independence can also be established by showing that P(club) = P(club | ace) = 1/4. You do not need
to do this, however, if you already proved P(ace) = P(ace | club) = 1/13 above. In other words, if event A is independent of B, then B is also independent of A.
(Finally, common sense prevails.)
Additional note: There is another equivalent check that you can perform. It
turns out that two events are independent iff the
probability of their intersection equals the product of their probabilities.
Students are often tempted to say P(A Ç B) = P(A)
· P(B), perhaps because they “learned” this rule in an earlier class.
THIS RULE IS NOT TRUE IN GENERAL. IT
IS TRUE IFF EVENTS A AND B ARE
INDEPENDENT. However, since “iff” means “if and
only if,” the rule is quite useful for checking for independence.
By this check P(ace
Ç club) = P(ace of clubs) = 1/52, and P(ace) · P(club) = (1/13) (1/4) = 1/52. Since the two answers are equal,
the events are independent.
|