Geometry / Mr. Hansen 12/1/2004

Name: __________KEY__________

Test on Chapter 5 (Short Answer Portion)

	Short answer (5 points each). No partial credit in most cases.
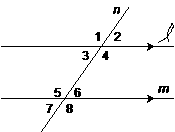
1.	Given: Distinct lines l, m, n with l || m, and n intersecting both of the other two.
	Make a sketch. Label the lines correctly (including tick marks), and label the 8 angles that are formed. Raise your hand so that I know that everyone’s numbers are compatible.
	I think everyone managed to do this. The only people who lost points were     those who forgot to write the lower case l in script style, or those who forgot     to number the angles. I think everyone remembered to mark lines l and m     with arrow ticks to indicate that they are parallel.
2.	List all pairs of angles that are congruent.
		Vertical angles: Ð1 @ Ð4, Ð2 @ Ð3, Ð5 @ Ð8, Ð6 @ Ð7 Corresponding angles: Ð1 @ Ð5, Ð2 @ Ð6, Ð3 @ Ð7, Ð4 @ Ð8 Alternate exterior angles: Ð1 @ Ð8, Ð2 @ Ð7 Alternate interior angles: Ð3 @ Ð6, Ð4 @ Ð5
3.	Suppose in #1 that it is not known that l || m. List all pairs of angles which, if known to be supplementary, would be sufficient to prove that l || m.
	Exterior SSOT: Ð1 supp. Ð7 Þ l || m Ð2 supp. Ð8 Þ l || m    Interior SSOT (same side of transversal): Ð3 supp. Ð5 Þ l || m Ð4 supp. Ð6 Þ l || m    Angles for which we have no category name: Ð1 supp. Ð6 Þ l || m Ð2 supp. Ð5 Þ l || m Ð3 supp. Ð8 Þ l || m Ð4 supp. Ð7 Þ l || m

Page 2 (E period version)
	Identify each quadrilateral without “overreaching.”
4.	All 4 sides are congruent.
	rhombus (by definition)
5.	There are two consecutive angles that are congruent.
	quadrilateral (for example, this could be a trapezoid, a square, or an “ugly nothing”)
6.	Diagonals bisect the quadrilateral’s angles.
	rhombus (a defining property of rhombuses, in fact)
7.	There is a diagonal that is the ^ bisector of the other.
	kite
	Always, Sometimes, Never.
8._A_	A square is a kite.
	Reason: All squares are kites, although not all kites are squares.
9._N_	An isosceles trapezoid is a rectangle.
	Reason: Trapezoids have only one pair of parallel opposite sides. Rectangles     have two pairs.
10._S_	A parallelogram has congruent diagonals.
	Reason: Although this can occur, it occurs only if the parallelogram is a rectangle.

Page 2 (version for most F period students)
	Identify each quadrilateral without “overreaching.”
4.	All 4 angles are congruent.
	rectangle (equiangular; can’t say “square” since equilateral was not given)
5.	There are two consecutive sides that are congruent.
	quadrilateral (for example, this could be a trapezoid, a kite, or an “ugly nothing”)
6.	Diagonals are congruent.
	quadrilateral (could be a rectangle, an isosceles trapezoid, or even an “ugly nothing”)
7.	Each diagonal is the ^ bisector of the other.
	rhombus
	Always, Sometimes, Never.
8._A_	A square is a kite.
	Reason: All squares are kites, although not all kites are squares.
9._S_	A rhombus is a rectangle.
	Reason: This can occur, but only in the case of a square.
10._N_	A trapezoid has diagonals that bisect all the angles of the quadrilateral.
	Reason: A quadrilateral in which all angles are bisected by diagonals is a     rhombus, and no trapezoid can be a rhombus.

Geometry / Mr. Hansen 12/2/2004

Name: _________________________

Test on Chapter 5 (Free Response/Computation)
5 pts. each for #6-13

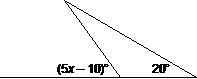
6.	Find the restrictions on x.     The exterior angle shown must be     greater than 20° but less than 180°.     By Algebra I inequality techniques,     we get 6 < x < 38. I was disappointed     to see that nobody solved this one.
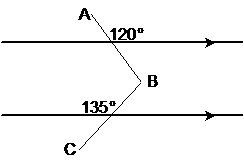
7.	Find mÐB.     Add an auxiliary line through B,     parallel to the other two parallel     lines. The total angle measure on     the left side of B can be shown to     be 105. (Some people were confused     about which angle is ÐB. However,     if you were to draw an auxiliary     segment connecting A and C, there     would be no possible ambiguity.)
8.	In this problem, you were given trapezoid EASY with segment EY and segment AS as bases. Given mÐA = 4x, mÐY = x + 60, and AS = x – 3, find AS. [Note: In the problem as originally written, the bars over EY and AS were correct, but the bar over AS was a typographical error since AS is a length, not a segment.]     Since base Ðs of an isosceles trapezoid are @, mÐS = 4x also. Since ÐS and ÐY are     interior SSOT (same side of transversal) for || lines, ÐS supp. ÐY. That gives us     4x + (x + 60) = 180, which we solve to get x = 24. Since AS = x – 3, AS = 21.
9.	Given: rhombus AHDR with diagonals intersecting at Y, perimeter = 52, and mÐHAR = 60 Find: HY [Again, there was a typographical error in the original, since HY is a length and should have no bar over it.]     Since perimeter = 52, and since AHDR is equilateral, AH = HD = DR = RA = 13. Since ÐHAR = 60° and DHAR is isosceles, DHAR must actually be equilateral, from which     we see that HR = 13. Since diagonals of a rhombus bisect each other (actually ^ bisect,     but we don’t need ^ here), we see that HY = 13/2 or 6.5.
10.	Given: Kite KITE, mÐ1 = 6x, mÐ2 = x + 20 [Note: There were two typographical errors in the original, since the “m” for measure was omitted twice.] Find: mÐIKE
	There was a huge error in the statement of this problem, namely that although KITE was given to be a kite, you were not told that the congruent sides were KI = KE and TI = TE. The diagram as originally drawn suggested that such was the case, but we cannot make assumptions based on the appearance of the diagram. However, since this was a mistake made by the textbook publisher, I overlooked it in scoring, and I gave full credit for solutions that assumed KI = KE, TI = TE. If we proceed with that (erroneous) assumption, then Ð 2 @ Ð3 by a property of kites. Since diagonals of a kite are ^, Ð1 is 90°, from which we get 6x = 90 Þ x = 15. Therefore, mÐ2 = x + 20 = 35, and mÐIKE = mÐ2 + mÐ3 = 35 + 35 = 70. On the other hand, if the congruent pairs of sides are KI = TI and KE = TE, then Ð3 is completely “stretchable” even while Ð1 remains 90° and Ð2 remains 35°. Thus it is impossible to compute mÐ3, and the real answer is insufficient information. Quite a few students set up an equation stating that mÐ1 = mÐ2. That, of course, is impossible, regardless of how one interprets the diagram. By properties of kites, the angles at point G are all 90°, and it makes no sense to say that Ð2 is also 90°. (If Ð2 were 90°, lines GE and KI would have to be parallel. However, the diagram shows those lines intersecting at I.)
	For problems 11 and 12, you were given a rhombus, with vertices T(3, 2), O(8, 2), P(11, 6), and S on the same y value as P. You were also given that the diagonals intersect at V.
11.	Find the coordinates of V.
	Since diagonals of a rhombus (indeed, of any parallelogram) bisect each other, V is the midpoint of segment TP. Remember your midpoint formula from several chapters ago? The coordinates of V are (xav, yav) = = (7, 4).

12.	Find the slope of segment SO.
	m = rise/run = Dy/Dx, what we call the “change in y divided by change in x” If you solved #11, you can find the slope of segment VO more easily. The change in y can be found by inspection (–2, a drop of 2 units) or by subtracting: 2 – 4 = –2. The change in x can be found by inspection as 1 unit or by subtracting: 8 – 7 = 1. Final answer: –2/1 = –2. However, note that you can solve #12 even if you could not solve #11. The y-coordinate of S is 6 by inspection, and the x-coordinate must bear the same relationship to T that P bears to O. Therefore, the x-coordinate of S must be 3 more than the x-coordinate of T. Therefore, S is the point (6, 6). Applying the slope formula again, we have m = = –2.
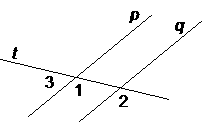
13.	Given: p || q, mÐ1 = 2x + 20, mÐ2 = 3x – 50 [Note: Again, there were two typographical errors in the original, since the “m” for measure was omitted twice.] Find: mÐ3
	Since Ð1 and Ð2 are corresponding Ðs, 2x + 20 = 3x – 50. Solving gives x = 70, from which we see that Ð1 and Ð2 are each 160°. The supplement, Ð3, has a measure of 20.
PROOF (10 pts.)	You were given scalene DPIG, with segment PT being the altitude to segment IG, and you were asked to provide an indirect proof (a.k.a. proof by contradiction) to show that segment PT could not be the median to segment IG.
	Assume (bwoc) that segment PT is the median to segment IG. Then        (1) IT = TG by def. median. We also know ÐPTI and ÐPTG are right Ðs (def. alt., def. ^). Therefore,        (2) ÐPTI @ ÐPTG since all rt. Ðs are @. Finally,        (3) PT = PT by the reflexive prop. Combining (1), (2), and (3) gives DPTI @ DPTG by SAS. However, that means that PI = PG by CPCTC. (®¬) (A scalene D cannot have two sides of equal length. Thus the proof by contradiction is complete.) [Shorter proofs are possible.]