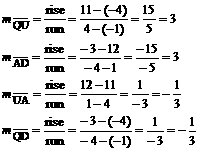Geometry / Mr. Hansen 2/18/2005

Name: _________________________

Answers to Chapter 9 Review Problems (pp. 429-433)

1.	(a) 9  (b) 8  (c) 5  (d)
3.	(a) 30  (b) on left, 5 on bottom  (c) 7  (d) 15  (e)   (f) 9 (g) on left, on bottom  (h) 25/2  (i) 26  (j) for both
5.
6.	5 km
7.	7 ft.
11.
12.
16.	(a) 8  (b) 7.5  (c) 8.5  (d) 8.5  (e) 7.5
17.	5 by distance formula Here is how to show the work (formula, plug-ins, and answer are required):
23.	After 3 hours, Boat A is 60 km north, and Boat B is 45 km west. These are legs of a 3-4-5 rt. D with a dilation factor of 15. Hypotenuse is 5(15) = 75 km.
24.(a)	Altitude is 6 by inspection. By ~ Ds, x/6 = 6/8. Solve (steps omitted) to get x = 4.5. Alternate method (easier): Since we have an altitude to the hypotenuse of a rt. D, we can use “near chunk, whole chunk” to get 10^2 = 8(8 + x). That means 100 = 64 + 8x Þ 36 = 8x Þ x = 4.5.
(b)	As in (a), we can use “near chunk, whole chunk” to get 6^2 = y(y + 9). That means 36 = y^2 + 9y Þ y^2 + 9y – 36 = 0 Þ (y + 12)(y – 3) = 0 Þ y = –12 or y = 3. We reject the negative length. Answer: y = 3.
27.	By 5-12-13 family, the rightmost unmarked segment is 5. By 3-4-5 family, the other unmarked segment is 4, which we can think of as 8/2 or “8 halves.” Since the side opposite x is 17 halves, x = 15/2 = 7.5 by the 8-15-17 family. No work is required.
28.	51 paces (see class notes for full explanation)
31.	The slopes of the 4 segments are as follows:
	Since there are 2 pairs of parallel sides, QUAD is a parallelogram. Since the adjacent sides meet with opposite reciprocal slopes, the angles are right. Therefore, QUAD is a rectangle. (Actually, after we know that we have a parallelogram, it suffices to check only one of the angles. If you have read this far, click here for a 2-point bonus opportunity.)