|
M
4/4/05
|
HW due:
(A period) None.
(E and F periods) If you have not already done so, write §10.9 #3, 4, 5, 9,
10, 16, 17. Apparently some people were confused by a formatting error in the
original posting of the assignment.
Optional interesting reading
assignment:
The U.S. Senate voted during the last
week before our spring break to allow oil drilling in the Arctic National
Wildlife Refuge (ANWR) in Alaska. The total amount of oil in the refuge is
estimated to be somewhere between 5.7 billion barrels and 16 billion barrels
(source: U.S.
Geological Survey report). During E period, Willie calculated that even
if the high-end estimate of 16 billion barrels is true, that is only about 3
years’ supply for the U.S., since our country uses about 20 million barrels
of oil per day.
Of course, ANWR would not provide 100% of oil needs; it would provide a
smaller fraction over a period of 30 years or more. President Bush, in his March
16 statement, correctly notes that ANWR oil would provide up to 1 million
barrels per day to America, making us less dependent on foreign sources of
energy. I wish that the President had gone one step further to calculate the
fraction of U.S. demand that ANWR would meet, which is about 1/20 or 5%.
There are a number of easy ways
to cut oil consumption by more than that, according to the NRDC, an
environmental group. In class, we discussed eliminating premium gasoline and
requiring tire-pressure sensors as two examples of ways to save several
percentage points. The NRDC article advocates using better tire and engine
technology to improve fuel economy, producing a much more dramatic reduction
in oil consumption.
When evaluating arguments of this type, you must critically evaluate the
source and weigh the evidence. The NRDC
article is essentially correct, but because it is written by an
environmental organization, the article presents facts to make a one-sided
case against the policy of ANWR drilling.
For example, the NRDC article uses figures of $28/barrel and $40/barrel for
future estimates of oil prices, as a way of explaining why the economically
recoverable reserves in Alaska may be lower than expected. However, if you
have been following the news recently, you know that oil prices have been
climbing higher and higher—which would increase the amount of economically
recoverable oil.
Needless to say, both sides in this debate are using biased reporting and
“selective statements of facts.” For example, the pro-drilling organization anwr.org has a Web page entitled “How Long Would Your
State Run With ANWR Oil?” That page shows that the District of Columbia
could operate for 1,710 years on the oil from ANWR, but that is an irrelevant
statistic, since the oil wouldn’t be earmarked for D.C. anyway. Buried deep
in the table is a fact that the pro-drilling organization probably didn’t
want anyone to see: Texas would run for only 9 years on ANWR oil, even if the
rest of the country received none.
|
|
|
T
4/5/05
|
HW due:
Review problems, pp. 505-508, {3i +
2 | i Î N, 0 £ i £ 7}. (In plain English, that means #2, 5, 8, 11, 14,
17, 20, 23.) Placeholders are permitted if you run out of time on the review
problems. Also finish §10.9 #3, 4, 5, 9, 10, 16, 17 if you have not already
done so. However, all problems in §10.9 are now required—no placeholders.
Remember, adequate work consists of a diagram plus formula, plug-ins, and answer with units. Bare answers, or
answers with inadequate justification, will not qualify.
During class: Outdoor project to measure the angle between the vertical and a
sloping line to the top of the Cathedral.
|
|
|
W
4/6/05
|
HW due:
Complete your §10.9 problems and all of the review problems previously
assigned, plus the following additional problem described below.
In E period, we computed the angle between the vertical and a sloping line to
the top of the Cathedral to be approximately 42 degrees. This was clearly a
mismeasurement. In F period, we achieved a much more accurate reading of 27
degrees. Your task is to (a) make a sketch, (b) compute the angle of
elevation, and (c) compute the height of the west towers of the Cathedral, to
the nearest foot. Show your steps. Use the 27-degree measurement obtained in
F period, plus the fact that the garbage can from which we made the
measurement is 100 feet from the base of the west towers.
Note: The Architectural
Facts page gives the actual height of the west towers as 234 feet.
Because of the inaccuracy of our crude protractor, your answer will not
match. Mr. Carroll has a good-quality surveying instrument that we might be
able to use in the future.
Extra Credit (optional): Work on the angle-arc puzzles written by the
Class of 2007. The best problem was written by Andrew’s older brother. These
problems make excellent review problems, in case you are looking for
additional challenging review problems.
|
|
|
Th
4/7/05
|
Test on Chapter 10 and Trigonometry. There will be one trigonometry problem, comparable
in difficulty to the calculation of the height of the Cathedral. To review
for the other problems, I recommend that you work on review problems from pp.
505-508 (either the ones we did, or better yet, some additional ones), Mr. Hansen’s angle-arc review puzzle, and/or
the angle-arc puzzles by the Class
of 2007. You need to know your “Rule of Half SAD” thoroughly!
Solutions to the angle-arc review puzzle
are now posted together with the puzzle itself.
|
|
|
F
4/8/05
|
HW due:
Write §11.1 #1, 3, 6, 8, §11.2 #1, 3, 4, 7, 8, 9, 14, 17. Reading is
optional.
In class (after speedy HW correction): Solar system model construction (1:10
billion scale).
|
|
|
M 4/11/05
|
HW due:
Read §11.3 (reading notes optional this time). It is an easy section, with
only one formula to learn. Write §11.2 #21c, 29, §11.3 #1-6 all, 17b.
You may copy the following solution to §11.3 #1 if you wish. However, the
problem is still required to be on your HW paper.
1(b). M = ½(b1 + b2)
= ½(15 + 11) = 13 units
1(a). A = Mh = 13(8) = 104 square units
Note: I did the two parts in
reverse order so that I could use the easier version of the trapezoid area
formula, namely A = Mh.
Extra credit (1 point; write answer on
your HW paper): Other than simplicity, why do I prefer the version of the
trapezoid area formula that I used in #1(a)?
|
|
|
T
4/12/05
|
HW due: Read §11.5 (incl. reading notes, as always); write
§11.4 #1-4 all, 7, 11 (by paper folding), 12 (by paper folding). Hint for
#7: Add to your diagram a certain circle whose diameter is 13.
|
|
|
W
4/13/05
|
No class (Diversity Day
during periods D, E, and F).
|
|
|
Th
4/14/05
|
HW due (50 minutes minimum in time log): Read §11.6; write §11.5 #1, 3, 5, 6, 15, 17, plus
the problem stated below.
The Pentagon, in Arlington, VA, covers a plot of land that is a regular
pentagon of side length 921 feet. Use trigonometry and the A = ½ap formula to compute the land area covered by the Pentagon. Show
your work.
|
|
|
F
4/15/05
|
HW due:
Read §11.7; write §11.6 #3, 5, 11-14 all.
In class (after we check HW): Geometry Jeopardy Bingo, F period only. E period
was too slow today for some reason. Lack of sleep? Too warm in the room?
We’ll have to try again another day.
|
|
|
M
4/18/05
|
HW due:
Reread the theorem on the middle of p. 544 (we have discussed this a number
of times previously); read and memorize
the two theorems on p. 550. Here, s
means semiperimeter (half the perimeter). Write §11.7 #2, 5-13 all, §11.8 #2,
3, 4, 6, 7. You may omit sketches for this homework only, so that a problem
such as #2 will take only a couple of minutes. As always, you must show the
setup of the problem (that is, you must state side lengths), and you must
show your work with answer underlined or circled. Compare your work against
the examples below:
§11.7 Example
2(a). s1/s2 = 5/2 Þ A1/A2 = (5/2)2 =
25/4 = 25:4
(b). s1/s2 = 6/9 = 2/3 Þ A1/A2 = (2/3)2 =
4/9 = 4:9 [it is a good idea to reduce before squaring!]
(c). s1/s2 = 8/4 = 2/1 Þ A1/A2 = (2/1)2 =
4/1 = 4:1
(d). s1/s2 = 2/6 = 1/3 Þ A1/A2 = (1/3)2 =
1/9 = 1:9
§11.8 Example
6(a). a = 3, b = 5, c = 6, s = (a + b + c)/2 = (3 + 5 + 6)/2 = 7
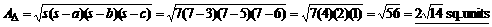
|
|
|
T
4/19/05
|
HW due: Work as many of the review problems on pp. 554-558
as possible. Focus on those that seem somewhat challenging to you, and keep a
time log. Answers with partial solutions are available by e-mail request. If
you need some suggested problems to work on, then (at a minimum) do #1-3 all,
5, 8, 13-17 all, 25-27 all, and 31. You will, of course, want to continue
working additional problems before taking the test.
|
|
|
W
4/20/05
|
Practice Test on Chapter 11. Everyone should
study for this, however. (See calendar entry for Friday 4/22.)
HW due: Additional review problems
from Chapter 11, or §12.1 #3, 7d, 8, 9, §12.2 #1, 4, 8, 11.
Let me explain what happened. F period voted to postpone the test until
Thursday. However, Thursday is Grandparents’ Day, which I should have
remembered but unfortunately did not remember until after everyone had been
dismissed. What a confusing situation! The way we will resolve this is to
have a practice test today (Wednesday) and to press onward into Chapter 12
until Friday.
|
|
|
Th
4/21/05
|
HW due:
§12.3 #1, 2, 4, 10, §12.4 #1, 2, 5, 9, 16. Also do the problems in §12.1 and
§12.2 if you have not already done so (§12.1 #3, 7d, 8, 9, §12.2 #1, 4, 8,
11).
Before school: It’s JBAM! In class:
Grandparents’ Day.
|
|
|
F
4/22/05
|
Actual Test on Chapter 11. If you are happy with how you did on Wednesday’s practice
test, you may take a day of rest today. If you take today’s test, it cannot
hurt the score you already earned on Wednesday. If you missed class
Wednesday—sorry, but you’ll have to take the test today.
|
|
|
M
4/25/05
|
FBK Day (no school).
|
|
|
T
4/26/05
|
HW due:
All previously assigned HW from §§12.1 through 12.4 will be collected
(quadruple scan). If you were not able to finish all the problems, you will
need a time log documenting 140 minutes of work, since you have had 4
weekdays since the assignment was originally made. However, frankly, 140
minutes should be adequate time to finish these problems. Remember that if
you are stuck, you can use the solution key that I distributed last week to
help you. (Don’t copy what I did; that would be an honor code violation.
However, you can learn from what I did and then work the problems in a
similar manner by yourself.)
If you have lost your solution key, please call a classmate. I also left
several copies taped to my office door. If you are on campus over the weekend
and can find someone to let you in, feel free to take one of those copies. If
you take the last one, please make a copy at Kinko’s so that one copy is left
for the next person.
|
|
|
W
4/27/05
|
HW due:
§12.5 #1-9 odd, 6, 10. Since this was not posted in a timely fashion, I
accepted HW written during class today.
|
|
|
Th
4/28/05
|
HW due:
§12.6 #2-10 even; read §13.1 and write #1, 4, 8, 9, 12 for a bonus point.
|
|
|
F
4/29/05
|
HW due: Read
§13.2; write §13.2 #4, 6, 9, 13-16 all. Also finish the problems from §12.6
and §13.1 if you did not already do so in class.
|
|