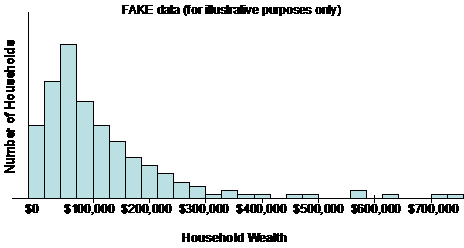Geometry / Mr. Hansen 2/2/2005

Name: _________________________

The Amazing Wealth of Bill Gates

Yes, yes, we have all heard that Bill Gates is the richest person in the world. However, few among us have a gut feeling for just how wealthy he is. Once the numbers get into the billions, they start to lose their meaning.

So . . . let’s put it in terms that we can all understand. As of 2000, the upper quintile (highest 20%) of American households had a median net worth of less than $200,000 (source: http://www.census.gov/prod/2003pubs/p70-88.pdf). Even today, with the substantial increases in home equity that have occurred over the past few years, it is a safe bet that the vast majority of American households have a net worth of $500,000 or less. Let’s go a bit higher, all the way up to $750,000 or so, and sketch a histogram that shows the distribution of wealth in America:

I have not marked any numbers on the vertical scale, since these data are notional (i.e., fake). The point I am trying to make is that the vast majority of all American households would fit on this graph. Only a tiny fraction of the population, the super-rich, would spill off the right edge of this chart, and the amount of blue that we would need to graph them would be negligible.

So far, so good. Let’s draw this histogram on the back wall of Room S, making it take up both blackboards there, and with the right end of the histogram trickling off to the right, i.e., northward. (In statistics, we would call this a skew right distribution.)

Keep in mind that almost every household in the country fits on this one blackboard. The question is, where does Bill Gates have his little tiny spot of blue if we were to extend this graph to the right?

Some people will guess Cactus Cantina, or maybe Bethesda, or Rockville. It’s actually a lot farther than that.

The blackboard is approximately 20 feet wide, and it represents a span of $750,000. We can set up a proportion to figure out how wide the graph would have to be to show a span of $1 million as follows:

Cross-multiply and solve for x. Answer: 26⅔ ft. is the width of a blackboard showing a span of $1,000,000.

Now, a billion dollars is a thousand million. That means that to show a span of $1 billion, we would need 26⅔ thousand feet, or a blackboard approximately 5 miles wide.

However, Bill Gates is not merely a billionaire. His net worth, as of 2/2/2005, is conservatively estimated at $60 billion (source: http://philip.greenspun.com/WealthClock). To show Bill Gates on the same blackboard with which we started, our blackboard would need to be 300 miles wide, since 60 times 5 equals 300.

Wow! That’s a huge blackboard. For what it’s worth, 300 miles would take us to the Canadian border near Niagara Falls.