|
1.
|
differential, integral, Fundamental Theorem
of Calculus, FTC
|
|
|
|
|
2.
|
limit, Riemann, 0
|
|
|
|
|
3.
|
rectangle, right, height, trapezoid (Trapezoidal Rule),
adaptive quadrature, faster
Adaptive quadrature uses a small mesh size only in
places where the function is changing most rapidly, i.e., where the small
mesh size provides the greatest benefit. In regions where the function is not
changing rapidly, wide rectangles (or trapezoids, or whatever) can be used to
achieve acceptable accuracy while saving time. Although Riemann sums for integrable functions become more accurate with decreasing
mesh size, it is a waste of time and processing power to use the smallest
mesh size everywhere.
|
|
|
|
|
4.
|
See footnote [1] at modd.net/abbrevs2.htm#FTC for a
statement of FTC1 and FTC2.
|
|
|
|
|
5.
|
See modd.net/23calc/handouts/ftc1and2.htm
for the proofs. Here are the justifications for the chains of equalities:
FTC1 Ž FTC2:
First equality is by FTC1 (assumed true by hypothesis).
Second is by properties of derivatives (deriv.
of diffs. = diff. of derivs., deriv. of a const. is 0).
Third is by def. of G
as an antiderivative of f.
FTC2 Ž FTC1:
First equality is by a property of definite integrals (splitting
at an intermediate point).
Second is by commutative property of addition (switching order of
addition).
Third is by another property of definite integrals (switching
limits causes change of sign).
Fourth is by def. of the accumulator function, H.
Fifth is by substitution, since we previously showed that "x, H(x) = G(x) – C.
Sixth is by algebraic simplification.
|
|
|
|
|
|
6.
|
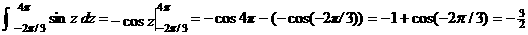
|
|
|
|
|
|
|
|
|
|
|
7.
|
If we let G(x) = ∫x–2.1 f (t)
dt + C, we will certainly have an antiderivative, since FTC2 guarantees that G′(x) = f (x). However, we must choose C so that G(–2.1) = –3.118. By
inspection, C must equal –3.118.
Answer: G(7)
= ∫7–2.1 f
(t) dt + C = 2,645,280.660 + (–3.118) = 2,645,277.542. [Note: A TI-83 or TI-83 Plus calculator
takes roughly twice as long to find the answer if you forget to specify e = .001 as the fifth parameter in MATH 9.]
|
|
|
|
|
|
|
8.
|
Note for both methods:
Total distance traveled = ∫010 |v(t)|
dt, but since
we know that rockets are fired upward, we can make the simplifying assumption
that v(t) ³ 0, thereby eliminating the absolute value bars. (If the problem had
asked for net distance traveled,
then it would be correct to eliminate the absolute value bars at the outset.)
Trapezoidal Rule:
∫010 |v(t)| dt = ∫010
v(t) dt
(by the note above; not true in general)
» ½ Dt (v(0) + 2v(2.5) + 2v(5) + 2v(7.5) + v(10))
=
½ (2.5) (0 + 20 + 50 + 80 + 60)
=
½ (2.5) (210)
=
262.5 m
Simpson’s Rule:
∫010 |v(t)| dt = ∫010
v(t) dt
(by the note above; not true in general)
» 1/3 (Dt) (v(0) +
4v(2.5) + 2v(5) + 4v(7.5) + v(10))
=
1/3 (2.5) (0 + 40 + 50 + 160 + 60)
=
1/3 (2.5) (310)
» 258.333 m
|
|
|
|
|
|