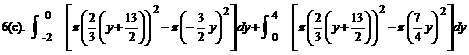Monthly
Schedule
(AP
Calculus AB, Period D)
|
T
3/1/05 |
HW due:
Read to end of §7.3 (omitting Exploration 2), and solve the following
problems: |
|
|
W
3/2/05 |
No additional HW due. |
|
|
Th
3/3/05 |
HW due: |
|
|
F
3/4/05 |
HW due:
Finish up all previously assigned problems, and add the following easy one: |
|
|
M 3/7/05 |
HW due:
Work the following review problems. 1.
Write a
paragraph in which you describe how to perform plane slicing to calculate
volume. Try to write this without referring to your notes or to the textbook. 2.
Let R be the circular region bounded by x2 + y2 = 16 in the xy-plane.
R is the base of a solid such that
each cross section (when the solid is intersected by planes perpendicular to
the x-axis) is an isosceles right
triangle. Each such isosceles right triangle has as one of its legs the
segment between the points (x, –(16
– x2)½) and (x, (16 – x2)½). Show that the volume of the solid
created in this fashion is 170⅔ cubic units. 3.
Explain the
formula V = ò 2pr h(r) dr, which is a formula that is sometimes useful for calculating volumes.
In other words, explain what 2pr represents, what h(r) represents, what dr represents, and what Riemann sum is
being invoked. 4.
What method is
represented by the formula V = ò 2pr h(r) dr? Is this formula required for the AP exam? 5.
For a regular
square pyramid, let s = side length
of square base, and let h = height,
i.e., the perpendicular distance from the apex to the plane of the base.
Several years ago, in geometry class, you learned that V = ⅓s2h for this pyramid. Use plane slicing
to prove the formula. If you can’t do this (because of algebra errors, or
whatever), then use plane slicing to prove that the volume of a regular
square pyramid having a 5-by-5 base and height 12 units equals 100 cubic
units. Do not use the formula from geometry; use plane slicing. (It does not
matter whether you use slices to create cross sections that are squares,
triangles, or trapezoids. However, squares are the easiest.) 6.
The right
triangular region bounded by the origin, the point (3, –2), and the point (7,
4) is revolved about the y-axis in
order to create a solid of revolution. A cross section through this solid, in
the xy-plane, would look like a bow
tie. a.
Solids of
revolution are important to study, in part, because they are commonly used in
the engineering of real-world objects. Why? Try to think of at least two
reasons. b.
Compute the
volume by radial slicing. (This is probably the easiest way. However, for
obscure reasons that are beyond the scope of our course, you must use as your
radius the value r = 10/3 since the
centroid of the triangle is located at (10/3, 2/3). If you have forgotten
what a centroid is, you could briefly review geometry. However, if you
prefer, you may simply use my value for the radius, compute the volume, and
move on. The answer is approximately 272.271 cubic units. If it takes you
more than a minute or two to compute that value with your calculator, I
expect to receive an e-mail message from you ASAP.) c.
Compute the
volume by plane slicing, using planes perpendicular to the y-axis. (This is probably how the AP
would suggest that you perform the task.) d.
Compute the
volume by cylindrical shells. (This is slightly easier than (c) but harder
than (b).) After you have worked these
problems, I strongly recommend that you work some additional problems to
build your proficiency and speed. There are many in the textbook, or you can
try an actual AP problem. Read problem
#1 from the 2002 exam as an example of what you are supposed to be able
to do in 15 minutes. (Note: Acrobat Reader is required in order for you to
view that link.) That’s certainly enough
problems to keep you busy, but here is another optional one that is fairly
interesting. Use the definition of average value of a function to prove that
if a regular square pyramid (see #5 above) is sliced with planar cross
sections parallel to the base, the average cross sectional area is ⅓
the area of the base. In class: Review. |
|
|
T
3/8/05 |
Test on §7.3 and Average Value of a Function. Note that §7.2 will in effect be tested again,
since many the volumes you compute involve calculating areas of cross
sectional surfaces, and frequently those cross sectional areas are
complicated enough to require the techniques of §7.2. (That is why §7.2
appears before §7.3.) |
|
|
W
3/9/05 |
No additional HW due today. |
|
|
Th
3/10/05 |
HW due (as announced in class): Read §7.4. Since this announcement was not posted
in writing until 8:45 p.m. Wednesday, I guess that technically you are exempt
from the reading assignment. However, don’t you have enough days off already
this week and next? It would make me happy if everyone had at least read the
section before class today. |
|
|
F
3/11/05 |
Day of rest (also last day
of third quarter). |
|
|
M
3/14/05 |
Career Day (no class). |
|
|
T
3/15/05 |
HW due: §7.4
#1, 5, 6, 21, 24, and the supplementary problem described below. For each
problem, show a sketch, your integral setup, and the calculator
answer correct to 3 decimal places. Do not attempt to use FTC1. |
|
|
W
3/16/05 |
HW due: Read
the statistics portion of §7.5 (toward the end of the section), and attempt
as much of the quiz as you can.
You may wish to consult with a STAtistics student—that would actually be
helpful review for them, since the AP Statistics exam is coming up in May. |
|
|
Th
3/17/05 |
HW due:
Repeat yesterday’s quiz with the
knowledge you now have. Try to get all of the problems correct. You may wish
to print out a clean copy for yourself. |
|
|
F
3/18/05 |
Last day of class before
spring break. HW due: Finish
reading §7.5 if you have not already done so (including reading notes).
Juniors are exempt from this requirement. No written HW for anybody. |
|
|
Week
of 3/21/05 |
Spring break. |
|
|
Week
of 3/28/05 |
Spring break. |
|
Return to Mr. Hansen’s home page
Last updated: 24 May 2005