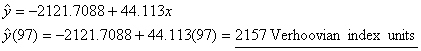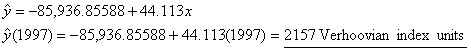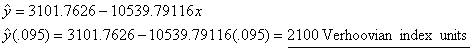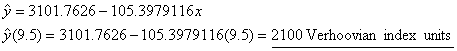AP Statistics / Mr. Hansen Test #2, 10/21/2003 (Chapters 3 and 4)

Name: _________KEY___________

Metaquestion: Why is a random guess in #1 through #6 better than playing a “hunch” if you don’t know the answer?

Answer: If you don’t know the answer, you are probably going to choose one of the “distractor” pitfalls that are set to capture the unwary. If you make a blind guess (using randInt, for example), your expected number of points earned is 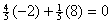, and since zero points on average will not help you, blind guessing is not likely to have much impact on your score. However, if you can positively rule out one of the choices and make a random guess from the four that remain, your expected number of points improves to 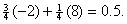If you can positively rule out two choices and make a random guess from the three that remain, your expected number of points becomes respectable: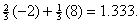

1.	B, since normalcdf(−2.5,−1.5)=.0606 Note: You can omit the third and fourth parameters, namely and , when you are using the “standard normal” values of 0 and 1, respectively. Also, although you cannot normally show “normalcdf” in your work (since it is considered calculator notation), work is not graded for multiple-choice questions such as this one. Since there is no partial credit, work is ignored.
2.	A The converse of the Empirical Rule is false. Simply because a distribution has 68% of its values in a band, 95% of its values in a band, and 99.7% of its values in a band centered on the mean, that does not mean that the distribution is normal. For example, the remaining .3% might be clustered at 20 standard deviations above the mean! N. N. Taleb (see question #6) made many millions of dollars by exploiting the fact that most Wall Street gurus and economists assume normal (Gaussian) models without questioning them.
3.	D
4.	D, since normalcdf(−99999,620,510,98)=.869
5.	B, since
6.	A We can systematically rule out all other choices. Taleb spends a large part of his book decrying Gaussian models (choice B), calling them the “GIF” (Greatest Intellectual Fraud) of all time. Taleb also has no patience for people who predict by extrapolating (choice C), nor does he put much faith in the “quantitative” part of quantitative risk analysis (choice D), except to profit from the blunders of people who underassessed their risk and sold options to Taleb at too low a price. Finally, Taleb profited in 2007-08 by betting against the soundness of credit-default swaps (choice E). Choice D is a good distractor, since Taleb is a mathematician and a risk analyst, but choice A is a better choice. As in all multiple-choice questions, you are supposed to choose the best choice.
7.	negatively
8.	a number that describes a population
9.	or population mean
	or population s.d.
	yes
10.	r^2
	explanatory
11.	strong negative linear [all three words are required]
12.	An r value close to 0 could result from a random cloud of data points. However, it could also occur (a) as the result of two or more clusters of strongly patterned points that cause a low r value when combined on the same scatterplot, or (b) as the result of a strong nonlinear pattern (e.g., quadratic or sinusoidal) that would almost completely cancel out any linear correlation.
13.	(a) r^2 = .776 = 77.6% for both parts, since r does not change if the roles of x and y are switched
	(b) r = −.881 strong, negative
	(c) r = .986 strong, positive
	(d) Using 2-digit years, with x = year, y = Verhoovian GP:
	Using 4-digit years, with x = year, y = Verhoovian GP:
	[Either method is acceptable, but you should clearly show which approach you followed.]
	(e) Using x = tax rate as a decimal (e.g., .095 = 9.5%) and y = Verhoovian GP:
	Using x = tax rate as a percentage omitting the % symbol, y = Verhoovian GP:
	[Again, either method is acceptable, but you should clearly show which approach you followed.]
	(f) Both involve extrapolation. In (d), we are extrapolating for a year into the future, and in (e), we are extrapolating for a tax rate for which we have no data.
	(g) Several possible responses are given below. There is no single “right or wrong” answer to this question. 1. Correlation, even strong correlation, does not imply causation. Since the Verhoovian economy grew in real terms during all but two of the periods shown (1981-82 had a 3.5% contraction of the economy, 1990-91 had a 2.1% contraction, but all other years were positive), one could reasonably dispute whether tax rates have an effect at all. The mere passage of time seems to predict growth. In fact, time is a better predictor of economic performance than tax rate, since the r^2 value for a time-GP model is (.986)^2 = .97, which is greater than the .776 found for the tax rate-GP model in part (a). [Although time is a better predictor, no cause-and-effect relationship can be inferred for time, either.] 2. Tax rates may be an effect rather than a cause. In other words, when the economy starts to falter, as it did in 1981-82 and again in 1990-91, the Verhoovian government may have to raise tax rates in order to avoid large revenue shortfalls and deficits. Then, when the economy improves, tax rates can be lowered because revenues are projected to be plentiful once again. 3. Both tax rates and GP are surely influenced by myriad lurking variables: laws, regulations, weather-related disasters, seasonal variations, fashion trends, influence peddling, conflicts of interest, etc. Finding any sort of repeatable pattern amidst all the noise, in the absence of a controlled experiment, is virtually impossible. 4. By cleverly choosing the case one wishes to make, one can torture this small table to say almost anything. For example, the average economic growth in years when the tax rate remained unchanged (2.9%) was the same as the average for years in which the tax rate was lowered from the previous year. Does that mean that there is no economic advantage to lowering tax rates and that the government should simply collect the additional revenue? Unfortunately, the question is not well posed; statistics cannot answer the question. If citizens are too poorly informed to consider the issue of lurking variables, then almost any data will suffice to make an argument, and demagogues will rule. The general reasoning fallacy is called post hoc ergo propter hoc (Latin for “after this, therefore because of this”). 5. Here is a really interesting lesson, one that you can hopefully avoid learning the hard way if you adhere to an “honesty is the best policy” way of life. You see, sometimes it happens that choosing an invalid model for self-serving reasons can be “self-correcting” in the sense that the model no longer makes the argument you wish it did. For example, despite the strong correlation (r = −.881) of the model that uses tax rate to predict GP, that model predicts GP in 1997 to be only 2100 units, a mere 0.4% growth from 1996. The model that uses calendar year to predict GP predicts GP in 1997 to be 2157 units, which is a much more robust (and politically popular) 3.1% growth rate over 1996. Thus imagine how the political debate might have proceeded in late 1996: Political Party A, arguing for lower tax rates, trumpets their model’s strong correlation and predicts 0.4% growth for 1997. Meanwhile, Political Party B says that Party A is full of hot air, and growth for 1997 should be 3.1%, based on a model that has stronger correlation, if tax rates are kept unchanged. If the political spin machine latches onto the (phony) distinction between 0.4% and 3.1%, it is clear who will win the debate. Imagine the ads: “The ______ Party wants you to live with only 0.4% growth next year. Maybe that’s good enough for them. But for working people, people like my family, that’s just not going to cut it. (Cut to voiceover announcer, the one with the “movie” voice.) Tell Your Legislator that You Won’t Settle for Four-Tenths of a Percent Either! Paid for by Citizens for Responsible Usage of Data.” Of course, lost in the shuffle is the fact that both A and B are using dubious models to perform extrapolation, and thus . . . they are both wrong.