Geometry / Mr. Hansen
2/11/2004


Check one:
(1 pt.)

                 Name: __________________________________
c Regular time (40 minutes, all problems)
c Extended time (48 minutes, omitting the “*” problems)

Test on Chapter 9 (through §9.8 only)

Instructions and Scoring. Please read carefully before you begin. Check (þ) each item as you read it (1 pt. each).

¨      Do not discuss this test with anyone except Mr. Hansen until next week. There are a number of students who may be taking make-up tests.

¨      There will be a 1-point deduction for each unnecessary disturbance during the test: speaking out of turn, asking a question that has already been answered, etc. If you have a question, please raise your hand and keep working until I spot you. This may take a minute. Please do not call out my name, since that creates unnecessary noise. If you see a typographical error, please mark it clearly for extra credit.

¨      No calculator is allowed. However, there is no difficult arithmetic on this test.

¨      Unless otherwise specified, leave all answers in simple radical form or a form involving p for full credit. If you have forgotten what simple radical form is, then leave your answer in any form you wish, and partial points will be awarded as appropriate.

¨      If you have regular time, your time limit is 40 minutes. Problems are 4.5 points each, plus 10 points for the instructions.
If you have extended time, your time limit is 48 minutes, and you should omit the problems marked with an asterisk (*). That leaves 16 problems worth 5.625 points each, plus 10 points for the instructions.

¨      Read the instructions for each part carefully.

¨      Diagrams are not necessarily to scale, and you should never assume conditions that are not stated. For example, do not assume that angles are congruent or that lines are parallel unless the problem explicitly says so.

¨      Please remember that there is an assignment posted on the Web for tomorrow.

¨      You may leave early if you wish. Please be very quiet.

 

 

Part I: Always, Sometimes, Never. Write the letter A, S, or N in each blank. Work is not required, but you may earn partial credit if you provide a diagram or a worthy explanation.

 

 

1. ___

The altitude to the longest side of a triangle has a length that equals the positive geometric mean between the lengths of the two segments into which that opposite side is divided.

2. ___

Assume a flat surface, and assume there are no tricks such as starting at the south pole. If a person walks 10 m due north, 20 m due east, and then another 10 m due north, then he or she will be 20Ö3 m from the starting point.

3. ___

If a regular square pyramid has sides of length 7 and an altitude of 7, then the slant height is 3.5Ö5.

4. ___

If a rectangular prism (box) has dimensions a, b, and c for length, width, and height, then the length of the long diagonal, d, satisfies the equation a2 + b2 + c2 = d2.

5. ___

If arc AB of circle C has measure 135, then area of sector ACB equals ¾ the area of circle C.

6. ___

An altitude to a side of a triangle is also a median.

 

7. ___

In a triangle having sides of length 3 and 4, the remaining side has length 5.

 

8. ___

If pentagon ABCDE ~ pentagon VWXYZ, then the ratio perimeterABCDE:perimeterVWXYZ is the same as the ratio CD:XY.

 

Part II: Free Response. Make a diagram for each question. The diagram is worth 3 points in most cases.

 

 

9, 10.

Let DABC be a right triangle with right angle at B. Let segment BD be the altitude to the hypotenuse. Let x = AD and y = CD. Give an expression for length BD.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

*11.

Show that the exterior angles of a regular octagon are each 45°.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12-15.

Let ABCDEFGH be a regular octagon with sides of length 8. Compute AD, AE, and the area of the octagon. If you cannot get one of the answers (e.g., AD) that is helpful in computing one of the later answers (e.g., AE), then you may clearly define a variable (e.g., x) that equals one of the previous answers and give your later answers in terms of x. If you need more than one variable, be sure to use different letters and mark everything clearly.

 

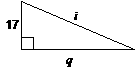
*16.

Write an expression that gives q.

 

 

 

 

 

 

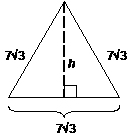
17.

Compute h.

 

 

 

 

 

 

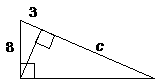
18.

Compute c.

 

 

 

 

 

 

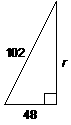
*19.

Compute r.

 

 

 

 

 

 

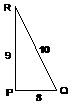
*20.

Classify DPQR as right, obtuse, or acute. Show your work (as always).