Geometry / Mr. Hansen 12/1/2003

Name: _________________________

Practice Test on Chapter 5 and PBT

	Part I: Always, Sometimes, Never. Write the letter A, S, or N in each blank (3 pts. each).
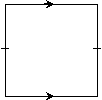
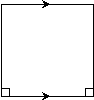
1. ___	If coplanar lines m and n are cut by a transversal in such a way that the exterior angles on the same side of the transversal are congruent, then m || n.
2. ___	A kite has perpendicular diagonals.
3. ___	A rhombus is a kite.
4. ___	A rectangle is both a parallelogram and a rhombus.
5. ___	In a kite, the diagonals bisect each other.
6. ___	In a parallelogram, the diagonals are angle bisectors.
7. ___	If a quadrilateral has congruent diagonals, then it is a rectangle xor an isosceles trapezoid. [Note: “xor” is not a typo. It means “or,” but in the exclusive sense, i.e., not “and/or.”]
8. ___	A kite with a right angle is a square.
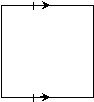
9. ___	If distinct coplanar lines l and m are each perpendicular to line n, then l || m.
10.___	Base angles of an isosceles trapezoid are supplementary.
11.___	If point Q is equidistant from the endpoints of a segment, then a line connecting Q to the segment is the perpendicular bisector of the segment.
12.___	If two coplanar isosceles triangles (either overlapping or back-to-back) share the same base, then the vertices of those triangles will determine the perpendicular bisector of the base.
13.___	If lines l and m are each perpendicular to line n, then l || m.
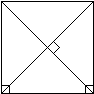
14.___	Let DABC be an isosceles right triangle with vertex at C. Let M be the midpoint of the hypotenuse, and let P be a point on segment CM. Then P is equidistant from A and B.
	Part II: “False Fixer-Uppers.” Each problem in this section (3 pts. each) is false. Your task is to mark up the sentence by inserting, changing, and/or deleting words so as to make the sentence true. However, you must make changes that reveal your knowledge of the subject—merely adding the word “not” is insufficient. Use a caret ( ^ ) to mark an insertion, and mark out any text to be deleted. The first one has been done for you as an example.
15.	If line l ^ plane m, then l is perpendicular to every line that lies in plane m. ^ ^and passes through the foot
	Note: You would earn no credit by changing the sentence to read, “If line l ^ plane m, then l is not perpendicular to every line which lies in plane m,” even though that modified version of the sentence is certainly true.
16.	Three points determine a plane.
17.	Two lines are parallel iff they never intersect.
18.	The following is a list of all possible ways that a sphere and a plane can intersect: (1) as a circle, (2) null set (i.e., no intersection at all).
19.	All of the following are possibilities for a quadrilateral that has two congruent consecutive angles: parallelogram, rhombus, kite, isosceles trapezoid.
20.	Write the most descriptive name that you can for the figure described in #19, i.e., a quadrilateral that has two congruent consecutive angles. ____________________________________________
	Part III: Free response. Use correct notation for all problems. Show your work clearly and circle your answer. Give fractions in lowest terms or decimals correct to 3 places, and include measurement units. Even if a problem can be solved by use of a calculator, show enough work so that your thought process is clear and so that you can earn partial credit if you make a mistake. Answers without work, even if correct, may earn no credit. (If you feel that no work is required, you may wish to write “by inspection” or “by insp.”; however, no partial credit is possible if you make a mistake.)
21.	(8 pts.) Two consecutive angles of a parallelogram are in a ratio of 5 to 3. Find the measure of the larger angle in degrees and minutes.
22.	(2 pts. each) Write the most descriptive name for each quadrilateral shown below. The diagrams are not necessarily to scale.
(a)		(c)
(b)		(d)
23.(a)	(5 pts.) Let the vertices of rhombus ABCD be as follows: A(3, –4), B(6, 0), C(11, 0), D(8, –4). Sketch ABCD on the coordinate plane, labeling the points.
(b)	(5 pts.) Calculate the slopes of the diagonals (segments AC and BD). Show your work. Hint: Remember that ABCD is a rhombus.
24.	(3 pts.) Why is the hint in #23(b) helpful for checking your work? __________________________________
25.	(14 pts.) Provide a 2-column proof to show that if the diagonals of a rhombus are congruent, then the rhombus is a square. Before beginning, write a diagram, the “givens,” and the “prove” statement.