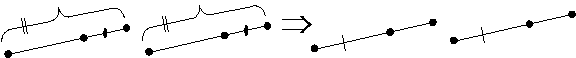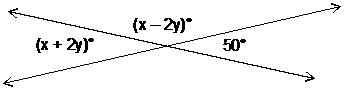Geometry / Mr. Hansen 10/9/2002, rev. 9/30/2003 and 10/28/2003

Name: _________________________

Practice Test on Chapter 2
Time Limit: 40 minutes (regular time students)

	Part I: Always, Sometimes, Never (3 pts. each). Write the letter A, S, or N in each blank.
1. ___	If two different (i.e., not congruent) angles are supplementary, then one of them must be obtuse.
2. ___	The ^ relation for lines satisfies the reflexive property.
3. ___	If an angle smaller than a straight angle is bisected, then both of the smaller angles formed are acute.
4. ___	If an angle smaller than a straight angle is bisected, then the smaller angles formed are complementary.
5. ___	The £ (“less than or equal”) relation satisfies both the reflexive property and the transitive property.
6. ___	In a pair of congruent triangles, or in any other pair of congruent figures, corresponding angles are congruent.
7. ___	If all corresponding angles are congruent between two triangles or any other type of figure, then the figures are congruent.
8. ___	Vertical angles are complementary.
9. ___	Two supplementary angles, Ð1 and Ð2, are each bisected to form two pairs of angles (i.e., four angles altogether). Let Ð3 and Ð4 denote the smaller angles formed by the bisection of Ð1, and let Ð5 and Ð6 denote the smaller angles formed by the bisection of Ð2. Then Ð4 is the complement of Ð5.
10.___	Let AB and XY be distances along straight segments, let C be a point between A and B, and let Z be a point between X and Y. If AC = XZ, then CB = ZY.
	Part II: Free response (pts. as marked). Use correct notation for all problems. Show your work clearly and circle your answer. Give fractions in lowest terms or decimals correct to 3 places, and include measurement units. Even if a problem can be solved by use of a calculator, show enough work so that your thought process is clear and so that you can earn partial credit if you make a mistake. Answers without work, even if correct, may earn no credit. (If you feel that no work is required, you may wish to write “by inspection” or “by insp.”; however, no partial credit is possible if you make a mistake.)
11. (10 pts.)	Two supplementary angles have the property that the larger one exceeds twice the smaller one by 15 degrees. Find the complement of the smaller angle.

12. (10 pts.)	Below is a wordless depiction of the Subtraction Property for Segments. In the blank space underneath the diagrams, write a wordless depiction of the Subtraction Property for Angles. (Or, if you prefer, you may write one or two complete sentences precisely stating the Subtraction Property for Angles.)
13. (20 pts.)	Make a diagram and write a complete two-column proof with numbered steps. Given: EBDC is a quadrilateral ÐABC is a straight angle             ray CA bisects ÐDBE Prove: ÐABD @ ÐABE
	___________________________________________________________________
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|

14. (10 pts.)	Essay. Using complete sentences, explain why “friendship” is not an equivalence relation.
15. (10 pts.)	By how much does x exceed y?
16. (10 pts.)	“A male drummer is well-paid only if he has good rhythm.”
(a)	Using letters, define the two statements that make up the conditional statement above. Let ____ = ________________________________________________ Let ____ = ________________________________________________
(b)	Write the quoted statement in English, using “if-then” format: _________________________________________________________________
(c)	Using letters and symbols, write the quoted statement as an implication: ____________________
(d)	Assume that the quoted statement is true. State the inverse using words or symbols (your choice): _______________________________________________________________ Is this inverse true? _______
(e)	Zeke is a drummer, but his rhythm is poor. What can we conclude? ___________________________________ Why? (Write a sentence or two, based on your knowledge of symbolic logic.)