Geometry / Mr. Hansen 9/13/2003 [rev. 9/22/2004]

Name: _________________________

Practice Test on Chapter 1

Time limit: 50 minutes. Choose a quiet work area and set a timer. No calculator allowed.

Part I: Always, Sometimes, Never (3 pts. each)

Partial credit is possible if you show work or provide a brief explanation. Write A if the given statement is always true, S if it is sometimes true, or N if it is never true.

___1.	Two supplementary angles are both acute.
___2.	A definition is a biconditional statement.
___3.	If the inverse of conditional statement S is false, then the converse of conditional statement S must also be false.
___4.	Theorems are reversible.
___5.	If P, Q, and R are distinct points satisfying PQ + QR = PR, then P, Q, and R determine a triangle.
___6.	If P, Q, and R are distinct noncollinear points, then PQ > |QR – RP|.
___7.	In spoken and written English, the word “is” means Û.
___8.	In spoken and written English, the words “only if” mean Ü.
___9.	Ray WX Ç ray WY = point W.

Part II: Essay (6 pts.)

10.	Explain why you cannot always compute the complement of the supplement of an angle, but you can always compute the supplement of its complement. (Use good grammar and clear wording. Complete sentences are not required; you may use sentence fragments if you wish.)

Part III: Creative Work (5 pts.)

11.

Write any two angles that you wish, using degree, minute, and second symbols, but make the larger angle be a whole number of degrees (0 minutes, 0 seconds), and make the smaller angle be a messy example with nonzero numbers of minutes and seconds. Subtract the smaller angle from the larger angle, showing your work.

Part IV: Problems (8 pts. for each numbered problem)

12.	Compute the angle between the hour hand and the minute hand of a clock at 11:47 a.m. Show a diagram and work. Give answer in xx°yy'zz" format (DMS).
13a.	Sketch DDOG having DO = 6 and DG = 8.
b.	Show the restrictions on OG with inequalities or a compound inequality. (Bigger than what? Less than what?)
c.	State the restrictions on OG with a mathematically correct English sentence that uses the word “between.”

14.	Make a diagram in which ÐABC is trisected by ray BD and ray BE. Compute ÐABC if mÐABD = 32¼. Give answer in degrees and minutes.
15a.	A rectangle whose sides are parallel to the x and y axes has vertices at (–10, 3) and (4, –6). Sketch the rectangle and the coordinate axes, labeling all 4 vertices.
b.	Compute the area of the rectangle. (Show formula for full credit.)
16.	Given: All gazelles are green. No green things are grimy. All grimy things are gross.
	Can we conclude that some gazelles are gross? ____ Justify your answer in some way.
Part V: Symbolic Logic (10 pts.)
17.	“We see aardvarks only when we are at the zoo.”
a.	(2 pts.) Using capital letters A and Z, define the two events that make up the conditional statement quoted above.
	____ = _______________________________________
	____ = _______________________________________
b.	(2 pts.) Restate the quoted conditional statement using mathematical notation.
c.	(1 pt.) Is your statement in part (b) true? ________
d.	(1 pt.) State the converse of the statement in part (b).
e.	(1 pt.) Is your statement in part (d) true? ________
f.	(2 pts.) Using mathematical symbols, write the contrapositive of the original quoted statement.
g.	(1 pt.) Now state the contrapositive of the original quoted statement using English only—no mathematical symbols.

Part VI: Proof (12 pts.)

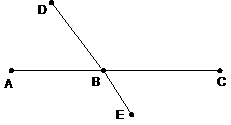
18.	Provide numbered steps and reasons. Write Q.E.D. or the Halmos sign () at the end to indicate that you have finished. Because this is not a homework problem, you do not need to rewrite the diagram, the “Given” statement, or the “Prove” statement. However, you do need to enter the givens as numbered statements in your proof.
	Given: ÐABC is a straight angle ÐDBA is supplementary to ÐABE Prove: ÐABC @ ÐDBE
	___________________________________________________________________
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|
	|