Geometry / Mr. Hansen March 2004 [rev. 3/15/2020; fonts corrected 2/16/2009, small error in Chris’s puzzle corrected 2/17/2009]

Name: _______________________

Angle-Arc Puzzles Created by Students and Mr. Hansen

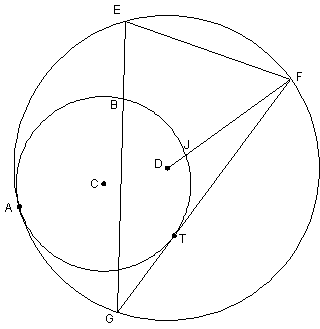
1.

Chris M.’s award-winning puzzle for 2004, edited by Mr. Hansen

Given: Circle E, = 65°, arc GF = 30°, arc GB = 110°, JC = 6, HP = 3, NK = 4 Find: , , , , , , , EB, EJ, EH, EK Note: The angles are straightforward, but finding the radius (EB or EC) is a bit challenging. Hint: EBJC is a kite. After you find EB (which equals EC), you should find that EJ, EH, and EK are not hard to compute. The original puzzle had JC = 7, but the diagram turns out to be impossible in that case. Using JC = 6 as above makes everything work out. If you would like a real challenge (probably suitable only for Algebra II students and above), try to compute AN, AP, and AE.

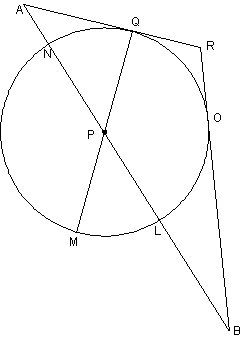
2.	An easier puzzle by Nico C. (edited by Mr. Hansen)
	Given: Circle P with points of tangency at Q and O, arc ML = 50°, arc LO = 75° Find: All arcs and angles Note: The original version of this puzzle had arc LO = 100°. Can you prove that that would be impossible?
3.	A puzzle by Mr. Hansen that is not hard if you look at it in the right way
	Given: Circles C and D, points of tangency at A and T, = 15°, EG = FG Find: