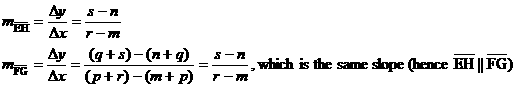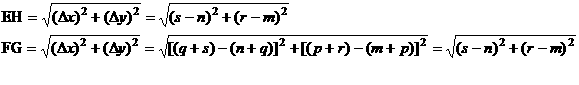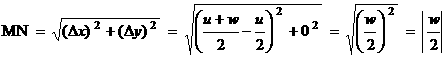Geometry / Mr. Hansen 5/23/2004

Name: ____________________________

Examples of Coordinate Geometry Proofs

	In a coordinate geometry proof, you begin by placing x and y axes on your diagram. You then mark the coordinates of the points of interest as variables, not as numbers, and you use algebra to prove whatever it is you are trying to prove. There will probably be a coordinate geometry proof on the May 2004 final exam.
1.	Use coordinate geometry to prove that the quadrilateral formed by joining the midpoints of the sides of any quadrilateral is a parallelogram.
2.	Use coordinate geometry to prove the Midline Theorem.
	Solutions
1.	Given: Quadrilateral ABCD, E mdpt. of , F mdpt. of , G mdpt. of , H mdpt. of Prove: EFGH is a
	Proof: Begin by placing points A through H on a coordinate grid. Wlog, we can simplify our lives by putting A at the origin. Also note (wlog) that since the segments have at most 8 different slopes, we can certainly rotate the figure if necessary so that none of the segments are vertical. [We need to avoid having undefined slopes.]
	Wlog, we must make no assumptions whatsoever about the shape of ABCD except that it is a quadrilateral. In fact, we do not even require that the figure is convex, even though the diagram above suggests that it is.
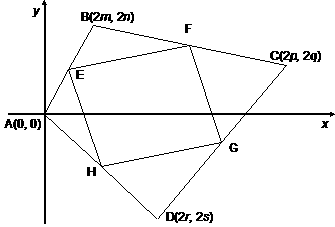
	We accomplish the generality by assigning coordinates to A, B, C, and D as letters. A is at the origin, of course, but points B, C, and D must be completely general. Knowing that we will need to compute midpoints later on, we can simplify our lives by calling B the point (2m, 2n) instead of simply (m, n). Here is our diagram now:
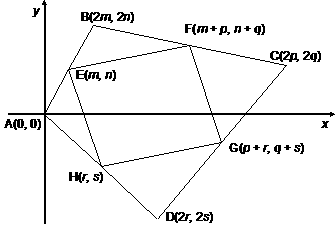
	Next, we apply the midpoint formula to determine the coordinates of E, F, G, and H as follows:
	To prove that EFGH is a , we need to show either 2 pairs of sides ||, or one pair of sides both || and @. In class on 5/21/2004, we used the first approach (2 pairs of sides ||), so for variety, let’s take the second approach now.
	By the distance formula,
	Since EH = FG, and since we previously showed the segments to be ||, EFGH is a . (Q.E.D.)
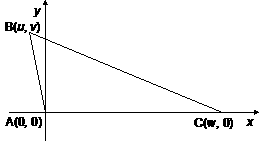
2.	Given: DABC with M mdpt. of , N mdpt. of Prove:
	Proof: Begin by placing DABC on a coordinate grid. Wlog, we can place A at the origin and C somewhere on the positive x-axis, but point B must be completely general. Because the choice of Quadrant II (as shown) or Quadrant I (if DABC is acute) for the placement of point B does not affect the computations that follow, the diagram below is still wlog. Also, having w > 0 is wlog.
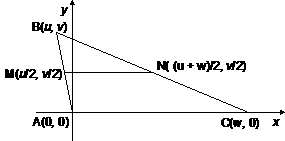
	Now use the midpoint formula to compute midpoints M and N:
	By inspection, both have slope 0 (horizontal segments) and are therefore ||. Or, we can make the proof a bit more airtight by noting that the change in y for the midline is v/2 – v/2 = 0. Since w > 0, the change in y, namely (u + w)/2 – u/2, is nonzero. Since 0 divided by any nonzero quantity is 0, the slope is 0. (Q.E.D.)
	For the second part of the proof, observe that AC = w by inspection. All we need to do is to show that MN = w/2. We can do this either by observing that N is to the right of M on a horizontal number line, by exactly w/2 units, or by applying the distance formula as follows:
	Since w > 0 by the initial placement of point C, the absolute value bars are not really needed here. We have MN = w/2 as required. (Q.E.D.)