AP Calculus AB / Mr. Hansen
3/10/2004


Check one:

           Name: ____________________________
c Regular time (12 + 12 minutes, all problems)
c Extra time (18 + 18 minutes, all problems)

Test on Chapter 8

Instructions and Scoring.

¨      Multiple choice only.

¨      Mark all answers on test sheet.

¨      No papers may leave the room. Initial ___________

¨      No additional HW for tomorrow. Remember, related rates were already due and may be scanned tomorrow.

¨      Without calc.: 6 problems in 12 minutes (18 minutes for extended time).

¨      With calc.: 4 problems in 12 minutes (18 minutes for extended time).

¨      No omissions for extended time (unless you are skipping the problem and are taking a zero for that problem).

 

 

Part I: Multiple choice, no calculator. The usual scoring rules apply. Mark the letter of the best choice.

 

 

1.

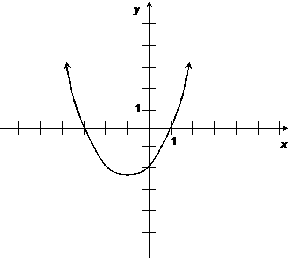
The graph of f ¢ is sketched below, and f ¢ is a parabola.

 

 

 

 

Which of the following must be true?

 

 

 

I.    f has a point of inflection when x = –1

II.   f has a relative maximum when x = –3

III. f is increasing when x = 0

 

 

 

(A) I only
(B) I and II only
(C) II only

(D) II and III only
(E) I, II, and III

 

 

2.

If the region enclosed by the x-axis, the curve , and the line x = 9 is revolved about the y-axis, the volume of the solid generated is

 

 

 

(A)
(B)
(C)

(D)
(E)

 

 

3.

The area of the region enclosed by the graph of y = 2x2 + 1, the line y = 3x, and the y-axis is

 

 

 

(A) 5/24
(B) 1/3
(C) 1/2

(D) 2/3
(E) 5/6

 

 

 

4.

How many critical points does the function  have on the interval (–1, 2)?

 

 

 

(A) zero
(B) one
(C) two

(D) three
(E) four

 

 

5.

What is the behavior of the function in #4 at the point (2, –8/3)?

 

 

 

(A) increasing
(B) decreasing
(C) stationary but not extreme

(D) at a local minimum
(E) at a local maximum

 

 

6.

The function y = (ln x + 1)2 has

 

 

 

(A) a single global minimum
(B) a single global maximum
(C) no global minimum or maximum

(D) negative concavity when x = 1/e
(E) a relative extreme point when x = 0

 

 

 

 

Part II: Multiple choice, calculator required. The usual scoring rules apply. Mark the letter of the best choice.

 

 

7.

The area of the region bounded by the curve y = tan–1 x and the line y = 1 in the first quadrant is closest to

 

 

 

(A) .5
(B) .501
(C) .502

(D) .503
(E) .504

 

 

8.

For the solid defined by having square cross sections built upon the base consisting of the region inside x2 + y2 = 1 (i.e., square cross sections when slicing perpendicular to the x-axis), the volume is closest to

 

 

 

(A) 4
(B) 5
(C) 6

(D) 7
(E) 8

 

 

9.

Let F be an antiderivative of . F(2) – F(1) is closest to

 

 

 

(A) .341
(B) .357
(C) .408

(D) .520
(E) .610

 

 

10.

The volume formed by revolving the region between  and the x-axis, for x Î [0, 3], about the line y = –1, is closest to

 

 

 

(A) 20
(B) 24
(C) 28

(D) 32
(E) 36