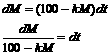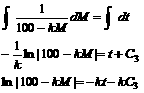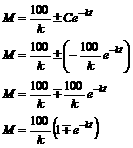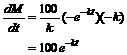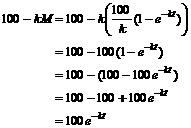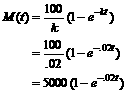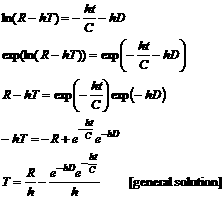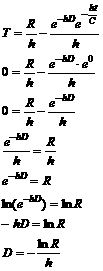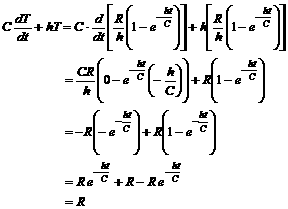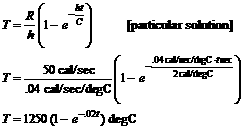AP Calculus BC / Mr. Hansen
1/23/2004 [rev. 1/28/2004]

 

Name: __________________________

Solutions to §7-3 #1, 4

1.(a)

The rate of change on the income side is +100 dollars/day. The rate of change on the expenditure side is –S dollars/day. Therefore, the overall rate of change dM/dt, is the combined total of these two. Answer: dM/dt = 100 – S. [Note: You cannot simply write 100 – S. You need to write the full differential equation as shown.]

 

 

 

(b)

In physics, we would write S µ M, meaning that S is proportional to M. In math class, we usually instead write

S = kM

where k is the constant of proportionality. Note: k > 0. When we substitute kM into the answer for (a), we get

dM/dt = 100 – kM.

 

 

(c)

The two important variables in this diffeq. are M and t, and you can tell that since the diffeq. involves dM/dt. “Separating the variables” means to get all the expressions involving M on one side and all the expressions involving t on the other. A diffeq. in which this can be done is called a separable diffeq., and although separable diffeqs. are by no means the only diffeqs. out there, they are the simplest to solve and do cover a wide range of real-world situations. In high school calculus, separable diffeqs. are the only type that we will learn how to solve exactly. For all other diffeqs., we will have to settle for approximation methods: slope fields and/or Euler’s Method, both of which occur later in Chapter 7. In college, if you take a diffeq. course, you will learn how to solve all sorts of diffeqs. using special tricks and techniques that are much more complicated than separating the variables.

The process of “separating the variables” is fairly straightforward, since dt is a number—in fact, as we learned previously, the independent variable t has differential dt, which equals Dt. [This is not true for dependent variables, but I digress.]

By algebra,

 

 

 

 

 

Is k a variable? No, k is one of those “adjustable constants” we often see in word problems, and we would say that k is a _____________ of the problem. Any solution we find for the unknown function M will be in terms of k.

 

 

 

Now antidifferentiate both sides:

 



 

 

 

             [Note: It is good to use a single “+ C3” on the RHS instead of C1 on the LHS and C2 on the RHS. But why do we use C3 and not simply C? Good question. That is because we want to keep C in reserve for later.]

 

 

 

Since we have a natural log on the LHS, we next perform an “e to the . . .” operation on both sides.

exp(ln |100 – kM|)= exp(–kt – kC3)
             [Note: “exp” means “e to the . . .”; we use exp whenever the exponent is complicated. Now, the LHS can be simplified since exp and ln are inverse functions, and the RHS can be rewritten by rules of exponents. When we modify both sides, we get the following equation.]
|100 – kM| = exp(–kt) exp(–kC3)
             [What sort of value is exp(–kC3)? That’s right, it’s a constant. We simplify by defining C4 = exp(–kC3). Note that C4 > 0 since e raised to any power is always positive.]
|100 – kM| = exp(–kt) · C4
|100 – kM| = C4e–kt
100 – kM = ±C4e–kt
– kM = –100 ± C4e–kt
             [Now, let C = –C4/k, and divide both sides of the eqn. by –k.]
M = 100/k ± Ce–kt

 

 

 

This was our goal: to find M as a function of the independent variable (t) and the parameter (k). However, this solution for M(t) is not very satisfying, because there is still an unknown constant C in the function. We call the solution shown above a general solution to the diffeq. because it still contains one or more unknowns. [Note: t is not an unknown; t is the independent variable. As discussed before, k is not an unknown; k is a parameter. However, C is a true unknown.]

What we really want is the particular solution to the diffeq. To get a particular solution, we must apply any initial condition knowledge that we have, and then plug in those facts in order to deduce what the missing constant(s) must be. By the statement of the problem, we know that t = 0 Þ M(t) = 0. In other words, the point (0, 0) is on the graph of function M.

Therefore, we plug (0, 0) into our general solution and see what happens:

M = 100/k ± Ce–kt     [general solution]
0 = 100/k ± Ce–k(0)
0 = 100/k ± Ce0
0 = 100/k ± C · 1
–100/k = ± C
C = –100/k or C = 100/k

Recall that we defined C = –C4/k above. We previously observed that C4 > 0, and at the beginning of the problem we noted that k > 0. Therefore, C < 0, and one of the two values for C stated above is impossible. We now know that

C = –100/k

and can plug that back into the general solution:

 

 

 

 

 

 

 

 

 

 

 

 

We are almost finished, but this last equation is two functions, not one function. Often, a diffeq. will have a multiple-function solution. However, this is not one of those times. The “+” sign in the second factor is impossible, since at (0, 0) that would give M = (100/k) (2), a positive value. We conclude that

 

 

 

 

Whew! After doing that much work, we must satisfy ourselves that we have a correct solution. The process of checking your solution is an essential step, and on tests I will not award full credit if you fail to verify that your solution satisfies the diffeq. (Sometimes the check fails, but then at least you know you have made a mistake.)

To “satisfy” a diffeq. means that the M solution you have found must make a true equation when plugged into the diffeq. itself.

Recall that our diffeq., way back in part (b), was dM/dt = 100 – kM. If our particular solution for M is correct, then we can compute the LHS of the diffeq. as follows:

 

 

 

 

 

 

Set that result aside, and now check the RHS of the diffeq.:

 

 

 

 

 

 

 

 

 

 

Hooray! A match!

 

 

(d)

 

 

 

 

 

 

(e)

See graph on p. 714.

 

 

(f)

M(30) » $2255.942 by calc.
M(60) » $3494.029 by calc.
M(90) » $4173.506 by calc.

You can calculate the income and expenditure amounts either by common sense or by calculus. Common sense is faster: After 30 days, $3000 has come in, and the difference between that and M(30), namely $744.06, is what has been spent. Similarly, after 60 days, $6000 has come in, and $2505.97 has been spent. After 90 days, $9000 has come in, and $4826.49 has been spent.

Calculus also works, and you should satisfy yourself that this is the case. Since the diffeq. has two components, namely a +100 income component and a –kM = –.02M expenditure component, we can define

I(t) = income accumulator fcn. = ò0t 100 du
E(t) = expenditure accumulator fcn. = ò0t (–.02M(u)) du

By calc., make sure that you can get the following:

I(30) = $3000
I(60) = $6000
I(90) = $9000
E(30) » –$744.058
E(60) » –$2505.971
E(90) » –$4826.494

 

 

(g)

M(365) » $4996.622 by calc.
Instantaneous rate of change = M ¢(365) » $.068/day by calc.

 

 

(h)

 

 

 

Reason: The second term in the second factor vanishes as t®¥.

 

 

4.(a)

R = C(dT/dt) + hT
Note that R is a constant.

 

 

(b)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[Note: Since hT, the rate at which heat is lost the room, cannot possibly exceed R, the rate at which the heater supplies heat, the absolute value bars are not needed in this problem. In general, you cannot throw away absolute value bars, but this time it is permitted. Always check carefully, and on the AP exam, supply a short reason. For example, write as an aside that R > hT since not all the supplied heat can be lost; hence R – hT > 0 Þ |R – hT| = R – hT.]

 

 

 

Continuing, we have:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Remember, as in #1, that to find the particular solution, we must use our initial condition information. The T function for temperature passes through the point (0, 0). T was defined as the heater’s difference (in °C) from room temperature. Actually, the problem does not clearly specify whether we are to use °C or °F for measuring temperature, but it is clear from the later context that °C is intended.

Continuing, we plug (0, 0) into the general solution as follows:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

With experience, you may note that solving for the integration constant D may not always be necessary. Here, the line that says
–hD = ln R is actually more useful, since it is e–hD that will be receiving the value of D in a moment anyway.

 

 

 

We substitute our newfound knowledge of D into the general solution:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Whew! As in #1, we need to check our solution against the original diffeq., namely R = C(dT/dt) + hT. We can do this by evaluating the RHS and verifying that we get R.

 

 

 

 

 

 

 

 

 

 

 

 

Hooray!

 

 

(c)

 

 

 

 

 

 

 

 

 

 

 

 

(d)

Now that you have the particular equation with values for all the parameters (part (c)), you can use your calculator to make the graph. Be sure to sketch the graph when you do your homework writeup. The shape is remarkably similar to the shape seen in #1(e), but this is not surprising, considering that the two functions have solutions of the same form.

 

 

(e)

By calc.,
T(10) » 226.587°C above room temperature
T(20) » 412.100°C     "         "        "
T(50) » 790.151°C     "         "        "
T(100) » 1080.831°C "         "        "
T(200) » 1227.105°C  "        "        "

 

 

(f)

Since e–.02t vanishes as t®¥, the limit is 1250°C above room temperature, by inspection.

 

 

(g)

By root finder or graph intersection finder, t » 230.259 sec. when T = .99(1250) = 1237.5.

The exact solution, using precal techniques, is t = –50 ln .01.