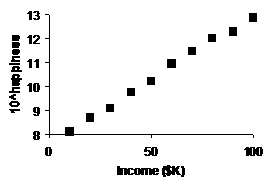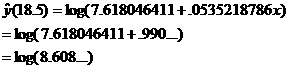Answer Key to Test on §§4.1-5.2
1. E [Barron’s book, 3rd ed., p. 476, #9] [older edition: p.
426, #9]
2. A [Barron’s book, 3rd ed., p. 453, #35] [older edition: p. 409, #35]
3. E [Barron’s book, 3rd ed., p. 454, #38] [older edition: p. 410, #38]
4. B [Barron’s book, 3rd ed., p. 481, #33] [older edition: p. 431, #33]
5.
|
Name of Bias |
Evidence for Existence |
Likely Direction |
|
Wording of the questions |
Question to students is a
2-part (conjunction) question; young boys may misinterpret how they should
answer. Lower Schoolers (in fact, anyone who has
not studied formal logic) may confuse “and” with “or.” Question to parents is
almost pathologically confusing and has some intimidation as well. |
For students, probably more
“yes” answers than would be found by splitting up the questions and counting
the students who answer “yes” to both. For parents, it’s anyone’s guess. |
|
|
||
|
Comment:
Technically speaking, wording of the questions is not a form a bias in this
problem, because the parameter of interest was given to be the percentages
who answer (i.e., who would answer) “Yes” to the questions posed. However,
after writing the question I realized that this was unnecessarily tricky,
teaches nothing of value, and serves only to confuse the issue. Therefore, I
accepted “wording” as a source of bias. |
||
|
|
||
|
Selection bias (undercoverage) |
Since only 2 surveys are sent
to each house, families with brothers in Lower School will be underselected (undercovered). |
Bias will decrease the % of
“Yes” responses [since families with more than 1 son enrolled are more likely
to be happy with STA]. |
|
|
|
|
|
Selection bias (overcoverage) |
If “Lower School” family
means any family that has a son enrolled in Lower School, then students who
live in 2 families (i.e., under joint custody arrangements) will be overselected (overcovered), as
will divorced parents. [Divorced parents get 2 surveys; married parents get
only 1.] |
Unpredictable. [Do
joint-custody families have a more favorable attitude toward STA? Who knows?] |
|
|
|
|
|
Hidden bias |
Students of Mrs. DeBord will probably be overrepresented, since they are
more likely to know where the collection box is. |
Unpredictable. |
|
|
|
|
|
Voluntary response bias |
Collection boxes are set up
in a rather inconvenient location for Lower Schoolers
and their parents (Steuart 203), so only those with
a strong opinion will take the trouble to respond. |
Bias will probably decrease
the % of “Yes” responses [since the satisfied people may see no need to
respond, and the upset people will go to any length to make their voice
heard]. However, it is also possible that the most satisfied parents and
students are those who spend a great deal of time on campus (volunteering,
involved with sports, etc.) and are therefore the most likely to visit Steuart 203 to deposit their survey. |
|
|
|
|
|
Response bias |
Lower Schoolers
may give positive responses because they think they should, especially if
their parents (who open the letter) hand them the survey. Parents may either
go along with the intimidating wording or may take a stand against it on
principle. Some parents, knowing that their sons will be dropping off the
survey, may be inclined to say “Yes” even if they don’t feel that way. |
Bias will probably increase
the % of “Yes” responses overall. |
|
|
|
|
|
Nonresponse bias |
Disorganized people, busy
people, families with two working parents, and families with older students
who have been at STA for several years [and have already received 0.4 billion
pieces of mail from STA] are all likely to be underrepresented since they are
less likely to see the mailing in the first place, let alone respond to it. |
Bias will probably decrease
the % of “Yes” responses [since these people tend to be fairly satisfied with
STA by default]. |
|
|
|
|
Other answers are possible for credit. You were required to give only four.
|
6. |
Because the greatest source
of variability is likely to be the students’ own geometry abilities, it makes
sense to use a matched pairs
design: Each subject serves as his own control. However, it makes no sense to
have the same person work the same questions twice, since a learning effect
can occur. Thus we need two quizzes of comparable difficulty and covering the
same geometric concepts. (A learning effect is still present, but greatly
diminished.) Since the order of administration (buzz first or buzz second)
and the quiz used (A or B) could be significant additional sources of
variability, we should block by these factors, creating four blocks in all. |
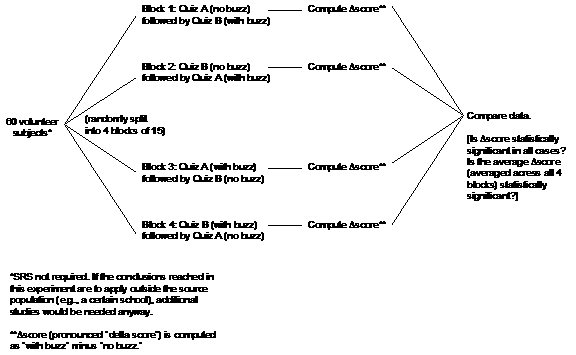
|
Control |
Blocking and matched pairs
[which is actually an additional type of blocking] assure that the presence
or absence of treatment (buzz) can be isolated as the only real change
affecting each subject, on average. |
|
|
|
|
Randomization |
Normally it is sufficient
to check simply that the assignment of subjects to treatments is random.
Here, each subject receives both treatment (buzz) and lack of treatment.
Since block assignment is random, the assignment of subjects to treatment
orders is also random. |
|
|
|
|
Replication |
We need enough subjects so that
the average difference in scores, which we expect to be negative, cannot be
criticized as being a “fluke.” [In the second semester, we will learn how to
calculate the required sample size in advance.] |
Note: This writeup is too detailed to fit into the 13 minutes that the AP exam allows for each free-response question. Although the exam also has one question that is about 25 minutes long, even that would be a stretch. I provided lots of additional detail here as an illustration of some of the issues you could consider. For good examples of shorter experimental design writeups, please see the Barron’s book.
|
7. |
|
|
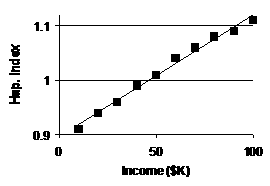
(a) |
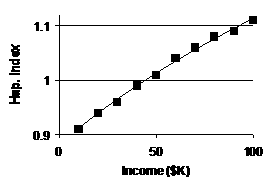
Scatterplot with LSRL overlaid: |
|
|
|
|
(b) |
Log curves “bend over” to
the right, i.e., show diminishing returns as explan.
vbl. grows.
It seems possible that happiness increases rapidly at lower income levels but
then takes more and more income to have the same effect as people grow
wealthier. [Or, it seems possible that the same ratio of incomes would produce the same incremental growth in happiness, which is the hallmark of
logarithmic growth.] |
|
|
|
|
(c) |
If we compute 10^(happiness) [i.e., 10 raised to the (happiness index)
power] and make a scatterplot against income, we get
a slightly more convincing straight-line pattern than the original: |
|
|
|
|
(d) |
Assume y » log(a
+ bx). |
|
|
|
|
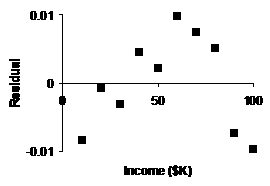
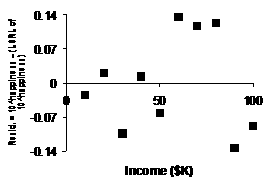
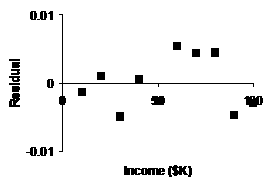
(e) |
Our Not only are these resids. smaller in absolute
value, but they show a more random scattering, which is good. Our new
shifted log model is superior. |
|
|
|
|
(f) |
By calc., orig. LSRL was yLSRL
= .896 + .0022363636x. |
|
|
|
|
(g) |
|
|
|
|
|
(h) |
Plot function |
|
|
|
|
(i) |
By same procedure in part (h),
required income would be about $384,250. |