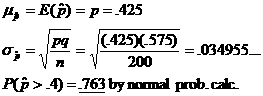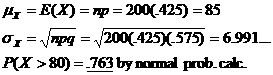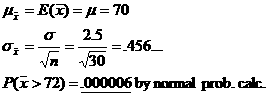|
AP Statistics / Mr. Hansen |
Name: _________KEY___________ |
Happy Quiz on Chapter 9
|
1. |
Suppose that the true proportion of registered voters in Springfield (pop. 3500) who support Mayor Quimby is 42.5%. In an SRS of 200 registered voters in Springfield, what is the probability that more than 80 support Quimby? Do this 3 ways: |
|
|
|
|
(a) |
Using a binomial approach for the count of 80; |
|
|
|
|
|
Let X = # of voters favoring Quimby in SRS of 200 |
|
|
P(X > 80) = 1 – P(X £ 80) = 1 – .261 by calc. = .739 |
|
|
|
|
|
|
|
|
|
|
(b) |
Using a normal-approximation approach for the sample proportion of .4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c) |
Using a normal-approximation approach for the count of 80. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Justify why parts (b) or (c) constitute a valid approach. |
|
|
|
|
|
Pop. (est. 2000 registered voters) is at least 10n = 10(200) = 2000 Ž trials are nearly indep., close enough to be considered binom.ü |
|
|
|
|
|
np = 200(.425) = 85 ³ 10ü |
|
|
nq = 200(.575) = 115 ³ 10ü |
|
|
(These last 2 rules of thumb verify that z approx. to binom. is valid.) |
|
|
|
|
3. |
STA students’ heights follow N(70, 2.5) (in inches). Find the probability that in an SRS of 30 students, the mean height exceeds 6 feet. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|