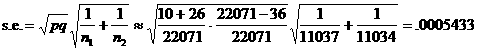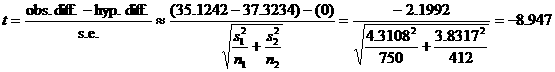AP Statistics / Mr. Hansen
4/4/2003

Name: _________________________

Key to Quiz on Chapters 11 and 12

Part I.

Each of the three parts (I, II, and III) involves a 2-proportion z test (STAT TESTS 6 on your calculator). We went over these problems in class in detail, but be sure to ask if you have any remaining questions.

 

 

1.

I.

P = .0076 Þ significant

 

II.

P = .000004647 Þ significant

 

III.

P = .1525 Þ not significant

 

 

2.

2 independent SRS’s from large populations (the theoretically infinite population of males 40 and older who could have been part of the experimental and control groups); no need to check 10n rule of thumb in this case, since this is an experiment ü

 

 

 

n1p1, n1q1, n2p2, n2q2 all ³ 5 for all three cases ü (success counts in table are all ³ 5, and failure counts are all over 10,000)

 

 

3.

Since H0 assumes p1 = p2, the sampling distribution of  (assuming H0 is true) will have equal variances. Let p denote the common value of p1 and p2, let q = 1 – p, and apply algebra to the first formula to get the second. We compute p, the pooled estimate of sample proportion, by dividing the total number of “successes” by the total number of subjects.

Alternate explanation: Since H0 assumes p1 = p2, the s.e. formula should logically make use of that assumption.

 

 

4.

 

 

5.

The answer to #4 is the s.e. of  (i.e., the difference between fatal heart attack sample proportions), assuming that the population proportions are equal.

 

 

Part II.

Many students wrote VHASTPC in the margin of the paper. Remember that this will mean nothing to the AP graders. Please either write VHASTPC on scratch paper, or (better yet) use the subheadings as shown below.

 

 

 

 

(a)

Vbls.: Let m1 = true mean score for students,
                 m2 =  "       "        "       "       experienced workers

 

 

 

 

 

H0: m1 = m2
Ha: m1 < m2

 

 

 

 

 

Assumptions: 2 indep. SRS’s from normal pops., unknown s’s. Nonnormality is OK here [see part (b)], and we treat subjects as coming from SRS’s of all possible experimental subjects. ü

 

 

 

 

 

[Optional sketch should be labeled "sampling distrib. of xbar1-xbar2, assuming H0 is true."]

Test statistic:

 

 

 

 

 

P value » 0 by calc. (underflow)

 

 

 

 

 

Conclusion: There is extremely strong evidence (t = –8.947, df = 933.57, P < .0001) that the true mean one-hole score for male college students is lower than the true mean for experienced female industrial workers.

 

 

 

 

(b)

Sample sizes here are large, and t procedures are robust for samples larger than about 40 even in the face of strong skewness.

 

 

 

 

(c)

Assume nearly normal distribution, approx. N(37.3234, 3.8317). By Empirical Rule, central 95% is approx. 37.3234 ± 2s, or approx. 37.3234 ± 7.6634, or (29.7, 45.0). [We could be more accurate, but the accuracy would be pointless since the distribution is only approximately normal anyway.]