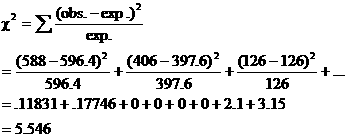AP Statistics / Mr. Hansen 4/18/2003

Name: __________KEY___________

Check for Understanding on Chapter 13

1.	Time limit: 20 minutes (30 for extended time).
	Slim Southpaw, a left-handed professional baseball pitcher, faced 1400 batters last year, 60% of whom were right-handed. No batter switched handedness during an at-bat. Of the right-handed batters, 70% were called out, 15% received a base on balls, 10% made a hit, and 5% were hit by Slim (i.e., advanced to first base). Slim’s overall record for the year was 71% out, 15% base on balls [note: this is a correction from the in-class version to make the numbers work out better], 10% making a hit, and 4% hit by pitch.
(a)	Is there evidence of an association between handedness of batter and at-bat outcome? If so, determine quantitatively (with a conditional analysis) where the differences are most significant.
(b)	Write your conclusion in AP Statistics terminology and again in plain language Slim could understand.
	BACKGROUND / DISCUSSION OF PROBLEM
	There are many wrong ways to do this problem. The wording intentionally involves a bit of misdirection, so that an unwary student might think he should conduct a c^2 goodness-of-fit test of the following null hypothesis:
		H0: pout =.71, pBB = .15, pbase hit = .10, phit by pitcher = .04
	Though perhaps plausible, that approach is invalid. When doing a goodness-of-fit test, you must compare against fixed claims of parameter values, not claims that are based in part on the data in the first category. Think “M&M’s proportions testing” when thinking about goodness-of-fit, and you should never go wrong.
	Another wrong approach involves an independence test (c^2 matrix test) claiming as its null hypothesis that the following data are independent:
	70	71
	15	15
	10	10
	5	4
	You must never do this! A c^2 test for homogeneity of proportions (or in this case, for independence since we have an entire population, not just an SRS) must use counts, not percentages. True enough, the null hypothesis is phrased in terms of the column percentages being homogeneous or independent, but the contents of the matrix itself must always be counts.
	A more sophisticated student might convert the percentages into counts (840 total for first column, and 1400 total for second column), producing a matrix that looks like this:
	588	994
	126	210
	84	140
	42	56
	This, however, is also wrong, since it is not a proper 2-way table. The second column must refer to a second category (viz., left-handed batters), not a marginal total.
	Finally, we realize that the following matrix is the appropriate starting point for the problem:
	588	406
	126	84
	84	56
	42	14
	What this means, of course, is the following table (note that I have added marginal totals and the grand total):
			RH batters	LH batters	Total
	Out		588	406	994
	BB		126	84	210
	Base Hit		84	56	140
	Hit by Wild Pitch		42	14	56
	Total		840	560	1400
	A marginal analysis of handedness of batters, based on the bottom marginal row of this summary table, would look like this:
			RH batters	LH batters	Total
			840 (60%)	560 (40%)	1400 (100%)

A marginal analysis of at-bat outcomes, based on the rightmost marginal column of the summary table, would look like this:
Out	994 (71%)
BB	210 (15%)
Base Hit	140 (10%)
Hit by Wild Pitch	56 (4%)
Total	1400 (100%)
(This percentage breakdown was actually provided as one of the givens of the problem.)
To perform a conditional analysis by handedness of batter, we must compute row percentages for each count in the body of the table (i.e., the percentage represented by each count, relative to its row total). The result is shown below. Note how the sum of each row is 100%.
	RH batters	LH batters
Out	588 (59%)	406 (41%)
BB	126 (60%)	84 (40%)
Base Hit	84 (60%)	56 (40%)
Hit by Wild Pitch	42 (75%)	14 (25%)
If someone asked, we could read the conditional probabilities of handedness directly from the table above: P(RH | out) = .59, P(LH | out) = .41, P(RH | base on balls) = .6, and so on.

We could also perform conditional analysis using column percentages, and the result is shown below. This table is much more useful in our case, because it is more likely that we would want to know the outcomes given the type of batter than that we would want to know the type of batter given the outcome. Note how the sum of each column is 100%.
	RH batters	LH batters
Out	588 (70%)	406 (72.5%)
BB	126 (15%)	84 (15%)
Base Hit	84 (10%)	56 (10%)
Hit by Wild Pitch	42 (5%)	14 (2.5%)
If someone asked for the conditional probabilities of outcomes, we could read them directly from the table above: P(out | RH batter) = .7, P(out | LH batter) = .725, P(base on balls | RH batter) = .15, and so on.
It is customary (and much simpler) to perform the marginal and conditional analyses at the same time. For example, here is the combined marginal and conditional table showing row percentages, i.e., percentages broken out by handedness. Note how each row adds up to 100%.
	RH batters	LH batters	Total
Out	588 (59%)	406 (41%)	994 (100%)
BB	126 (60%)	84 (40%)	210 (100%)
Base Hit	84 (60%)	56 (40%)	140 (100%)
Hit by Wild Pitch	42 (75%)	14 (25%)	56 (100%)
Total	840 (60%)	560 (40%)	1400 (100%)

	Here is the combined marginal and conditional table showing column percentages, i.e., percentages broken out by type of at-bat outcome. Note how each column adds up to 100%. In our case, this table is definitely the most useful way to view the data.
			RH batters		LH batters	Total
	Out		588 (70%)		406 (72.5%)	994 (71%)
	BB		126 (15%)		84 (15%)	210 (15%)
	Base Hit		84 (10%)		56 (10%)	140 (10%)
	Hit by Wild Pitch		42 (5%)		14 (2.5%)	56 (4%)
	Total		840 (100%)		560 (100%)	1400 (100%)
	ONE POSSIBLE “VHATPC” SOLUTION TO THE PROBLEM
(a)	H0: Handedness of batter is indep. of at-bat outcome. Ha: There is some assoc. betw. handedness & outcome.
	Assumptions: Counts from a pop., all exp. counts ³ 5 ü
	[You could also use green box on p.734, but those take slightly longer to state.]
	Exp. counts (each cell = rowtot · coltot/grandtot)
	994 · 840/1400 = 596.4			994 · 560/1400 = 397.6
	210 · 840/1400 = 126			[etc.] 84
	84			56
	33.6			22.4
	Test statistic
	P = .136 by calc.
	Concl.
	There is insufficient evidence (n = 1400, df = 3, c^2 = 5.546, P = .136) of an overall association between handedness and at-bat outcome. [See additional notes at end.]
(b)	AP Statistics terminology: Despite the fact that Slim was twice as likely to hit the batter when the batter was right-handed instead of left-handed, there is only very weak evidence (P = .136) of an overall association between batters’ handedness and at-bat outcome. The differences seen could plausibly have been caused by chance. Plain language version: “Slim, you need to be careful not to hit those right-handed batters. Last season, you beaned lefties only about 1 time in 40, but you beaned righties twice as often. But overall, your results when facing righties or lefties seem fairly random.”
	ADDITIONAL NOTES
	As worded, the question does not require an explicit conditional analysis at the end of part (a). However, the conditional analysis is still interesting. The contributions to c^2 (easily computed by hand or with the CSDELUXE program for your TI-83) are as follows:
	.11831	.17746
	0	0
	0	0
	2.1	3.15
	The absolute differences between expected and observed outcomes are about 8 in all 4 cases where the contribution to c^2 is nonzero. However, only the last row contributes a meaningful amount to c^2. In other words, the proportion of batters struck by wild pitches seems to be the only place where handedness of the batter makes any real difference.
	The relevant conditional probabilities (see earlier background/discussion of problem) are P(batter hit by wild pitch | RH batter) = .05 P(batter hit by wild pitch | LH batter) = .025
	If handedness were independent of at-bat outcome, we would expect the values to be equal, certainly not differing by a factor of 2. Note that in this problem, we have to use column percentages to make the point clear; using row percentages and observing that P(RH batter | hit by wild pitch) = .75 and P(LH batter | hit by wild pitch) = .25 is not nearly as convincing, since we would expect those numbers to be unequal anyway. (After all, Slim faced mostly right-handed batters during the season.) In a different problem, it might be that you would need to use row percentages to make the point clear, but here the column percentages are certainly better.
	Keep in mind that the purpose of a c^2 test for independence is to see whether there is any overall evidence of an association between two categorical variables. We have been treating the data as a population, not an SRS. The follow-up analysis presented below should not be used on the AP, but it is interesting to see how it plays out.
	If we let p1 = true proportion of right-handed batters hit by Slim, and p2 = true proportion of right-handed batters hit by Slim, then a 2-prop. z test of the hypotheses
	H0: p1 = p2 Ha: p1 ¹ p2
	yields a P-value of .019, suggesting statistical significance. Strictly speaking, this is not a valid procedure, since now we are reclassifying our data as being “2 independent SRS’s of all possible right- and left-handed batters Slim could have faced during the season,” but the results are nevertheless striking. A similar 2-prop. z test conducted using the proportions of RH and LH batters receiving an out (sample proportions 588/840 and 406/560) yields an unimpressive P-value of .313, clearly not significant.
	In other words, our observation of where the largest contributions to c^2 occurred matches well with our notions of which conditional probabilities differ to a statistically significant degree.